多重帰還型アクティブフィルタの特性と設計計算
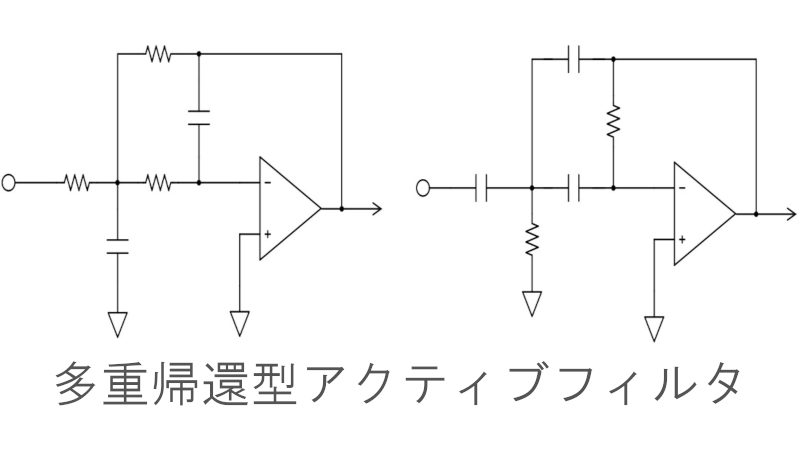
本稿では多重帰還型のアクティブフィルタについて解説していきます。
前回までに紹介したサレンキー型アクティブフィルタは非反転増幅回路となっていましたが、多重帰還型では反転増幅回路となります。
サレンキー型2次フィルタの特性と設計計算
サレンキー型3次フィルタの特性と設計計算
ローパスフィルタ(LPF)
多重帰還型のローパスフィルタはこのような回路です。
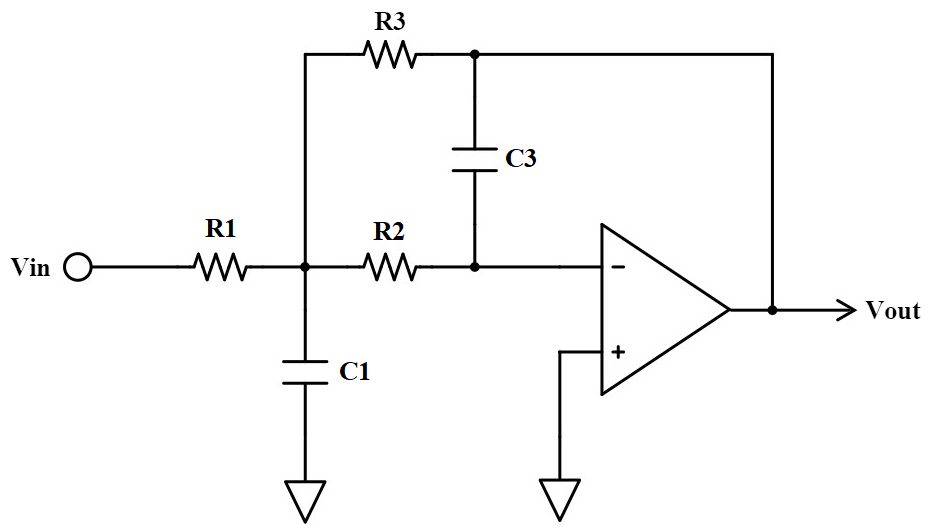
伝達関数、カットオフ周波数、Q値は以下の式で表されます。
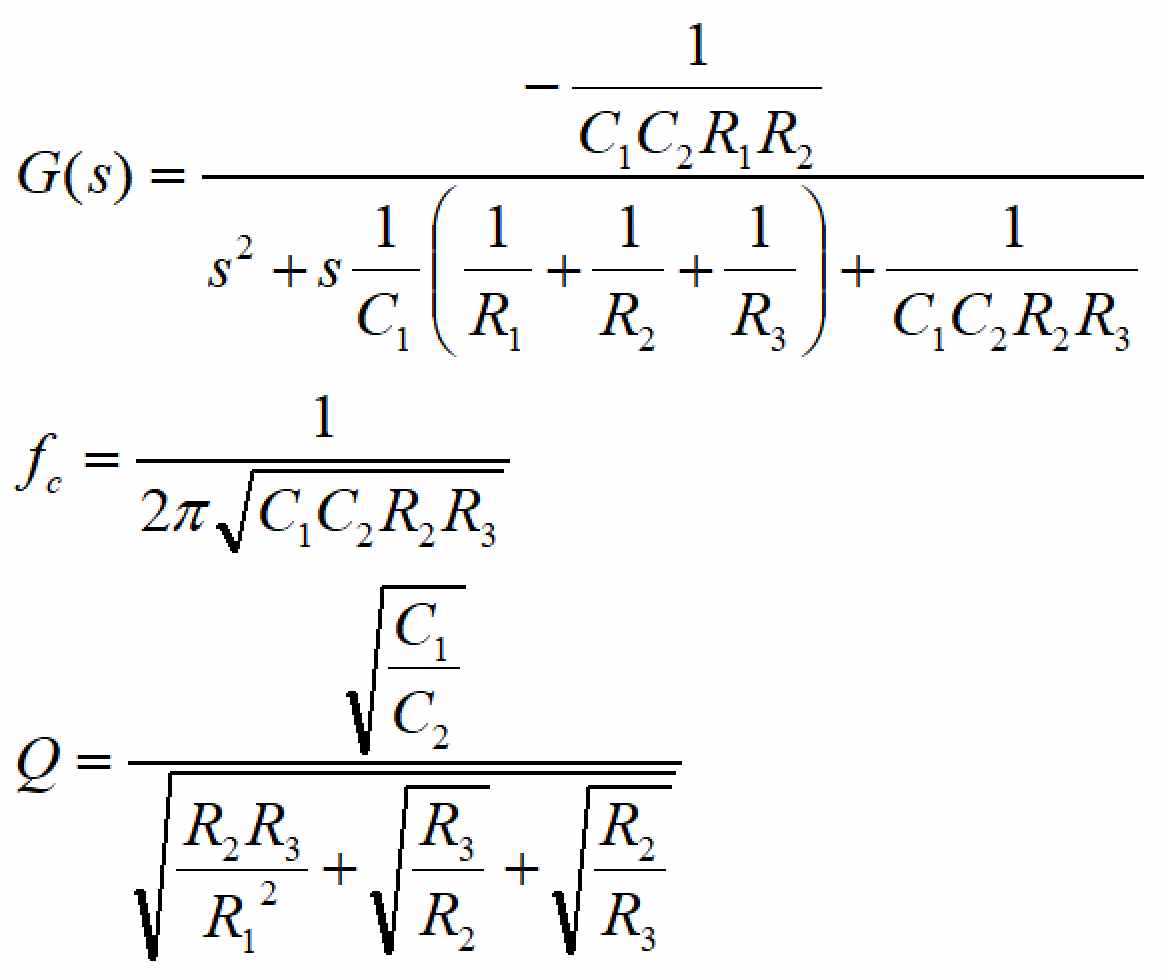
設計計算
計算を簡単にするため、R1=R2=R3=R、Q=1とすると、
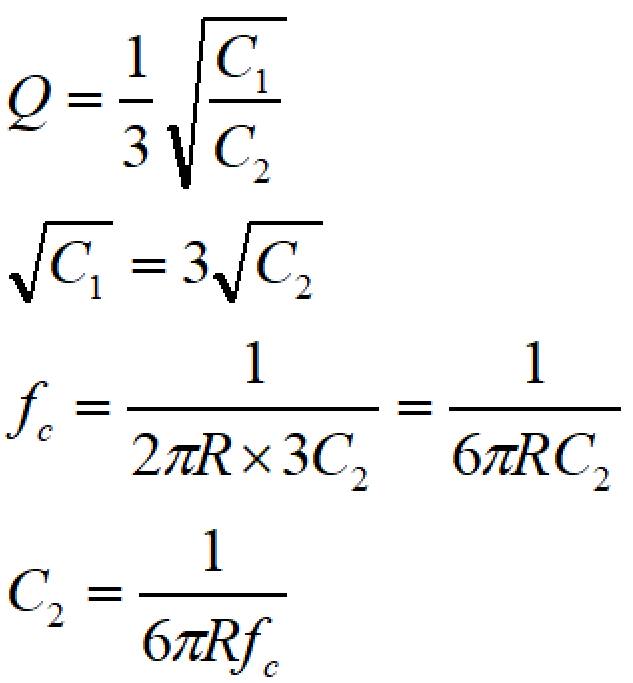
となります。
R=10kΩ、fc=1kHzとすると、
C1=47nF、C2=5.3nFと計算できます。
周波数特性
上記定数の周波数特性をLTspiceで確認してみます。
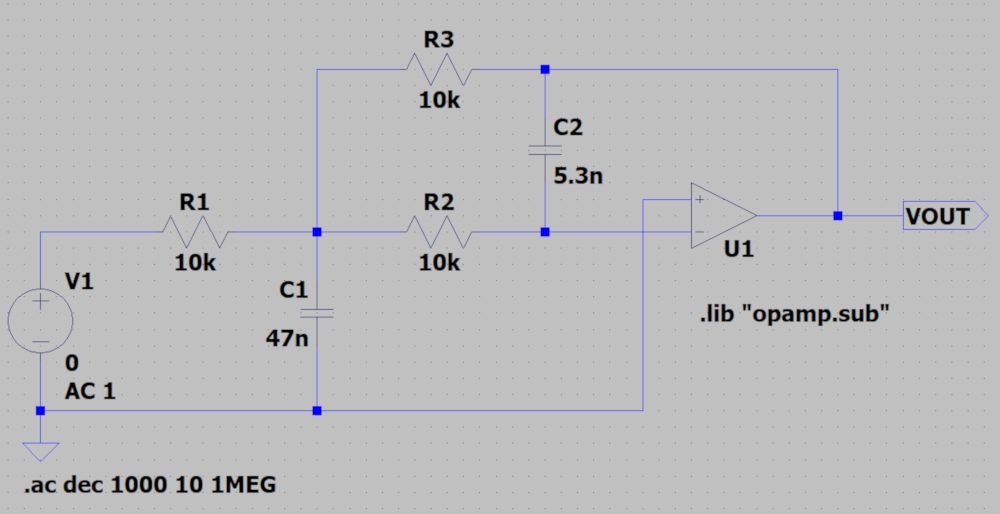
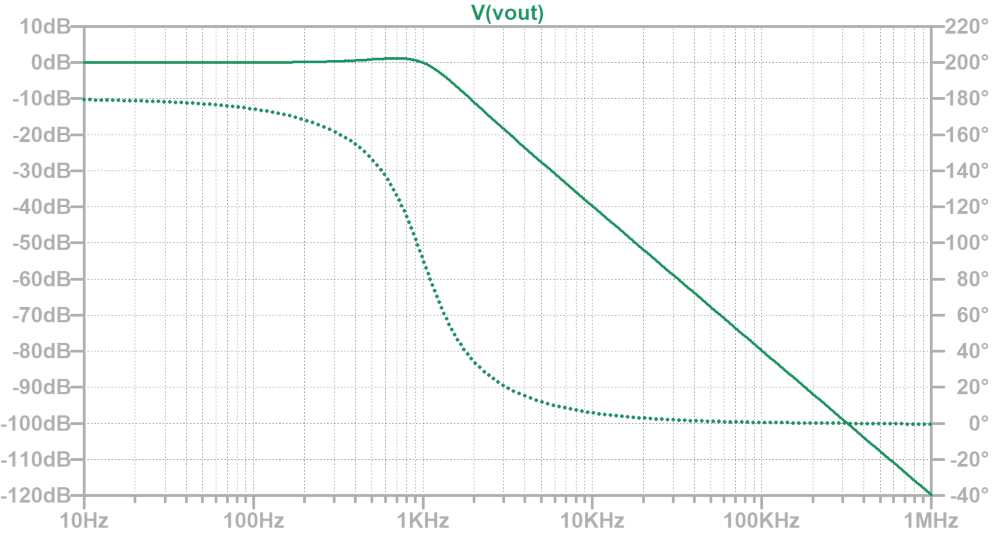
減衰特性は-40dB/decadeとなっていることが分かります。
増幅率
増幅率Kは
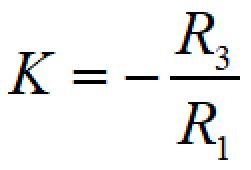
で表されます。
KはDC(0Hz)での利得です。
R1=R3であれば、K=-1となるので-1倍(0dB)となります。
ハイパスフィルタ(HPF)
多重帰還型のハイパスフィルタはこのような回路です。
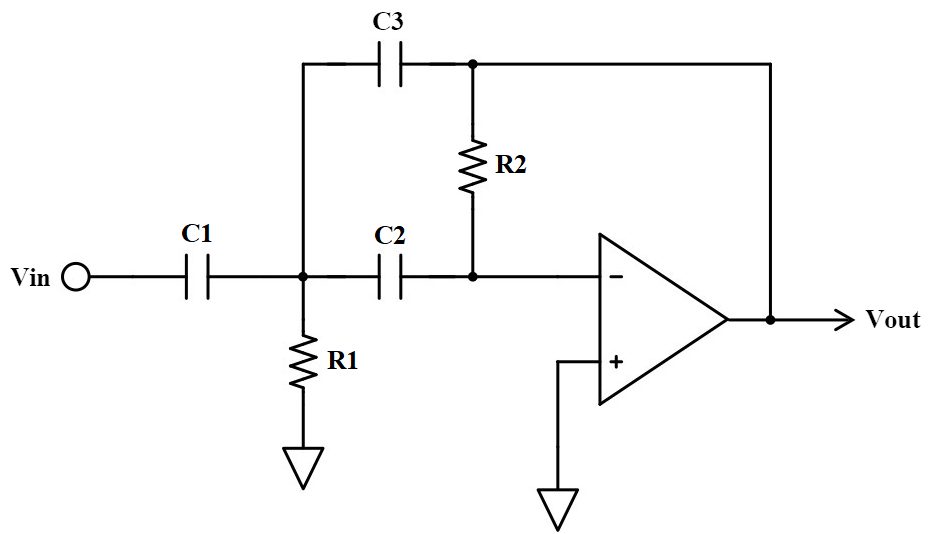
伝達関数、カットオフ周波数、Q値は以下の式で表されます。
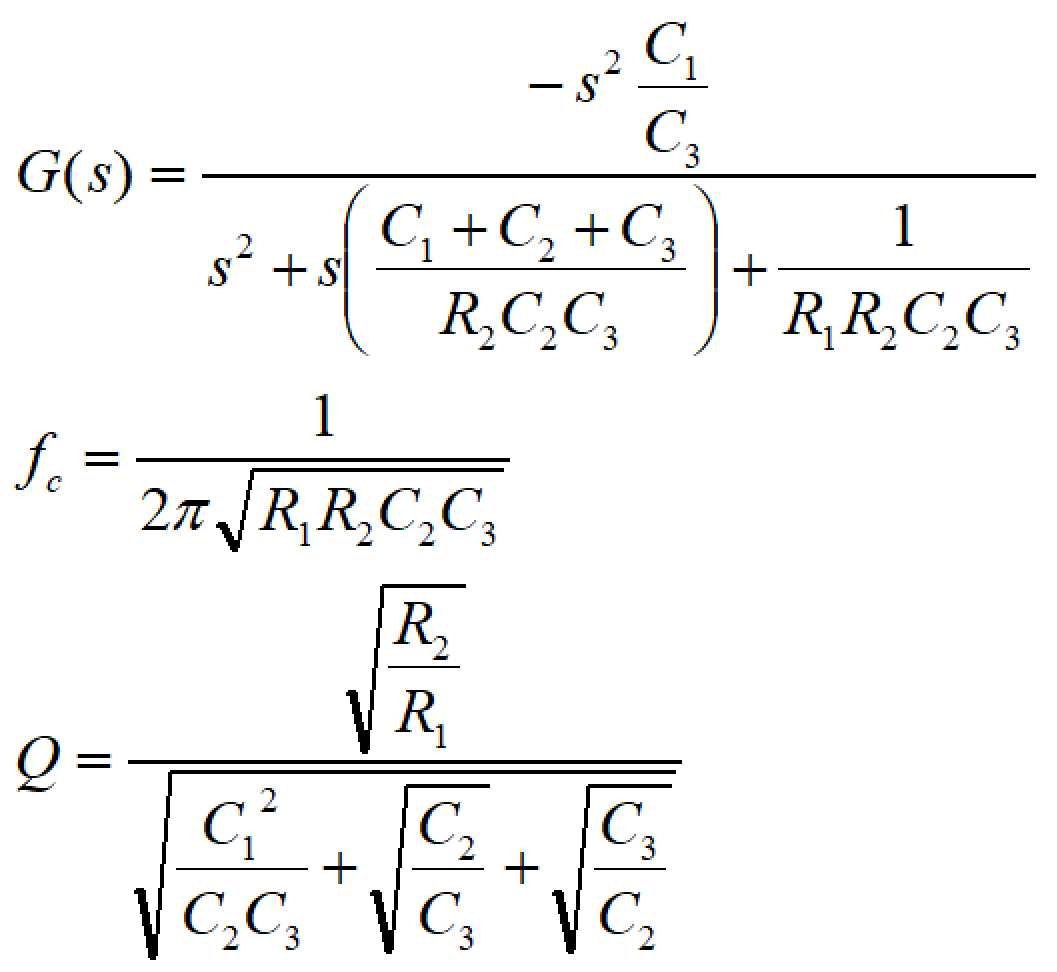
また、fc=∞でのゲイン:Kは
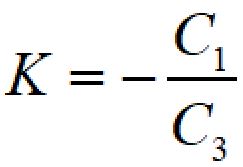
で表されます。
設計計算
計算を簡単にするため、C1=C2=C3=C、Q=1とすると、
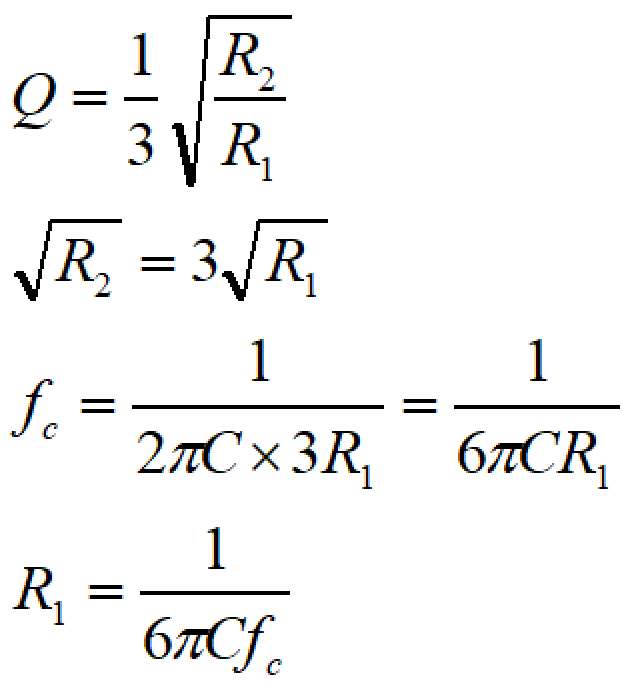
となります。
C=10nF、fc=1kHzとすると、
R1=5.3kΩ、R2=47kΩと計算できます。
周波数特性
上記定数の周波数特性をLTspiceで確認すると以下のようになります。
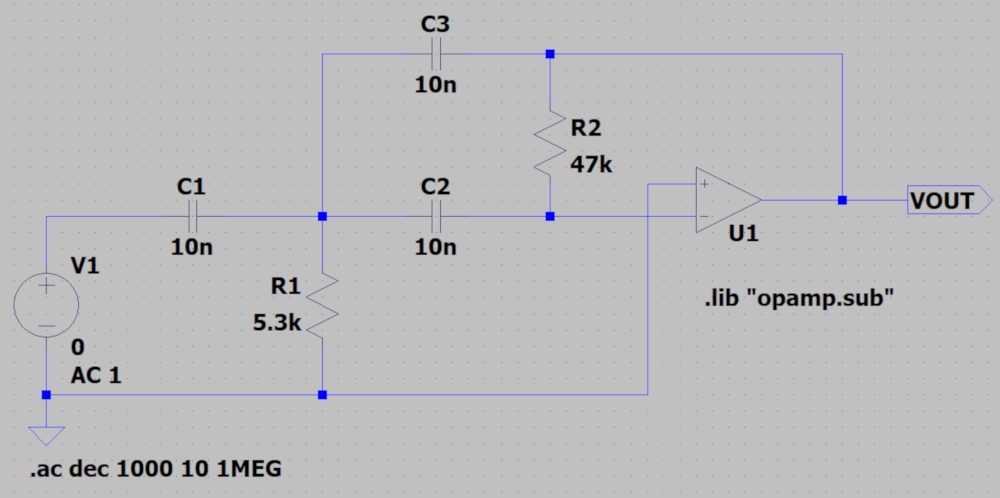
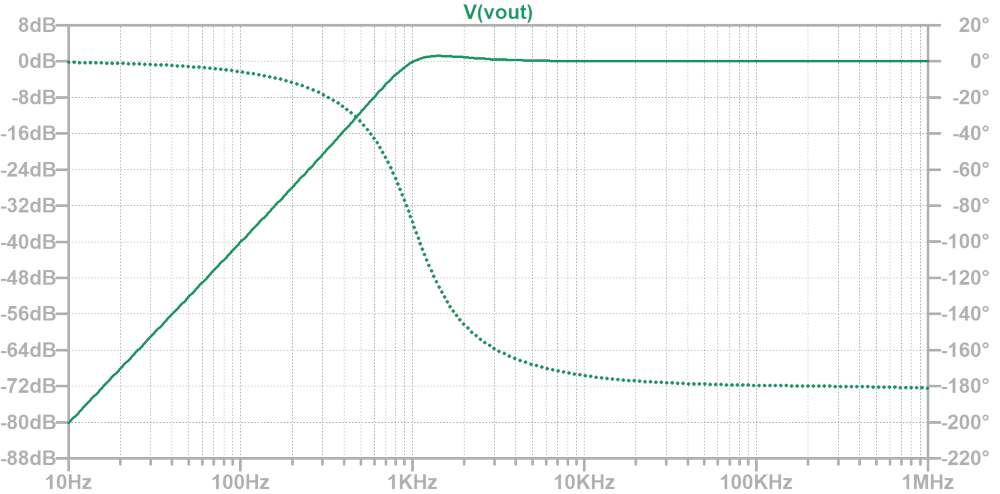
バンドパスフィルタ(BPF)
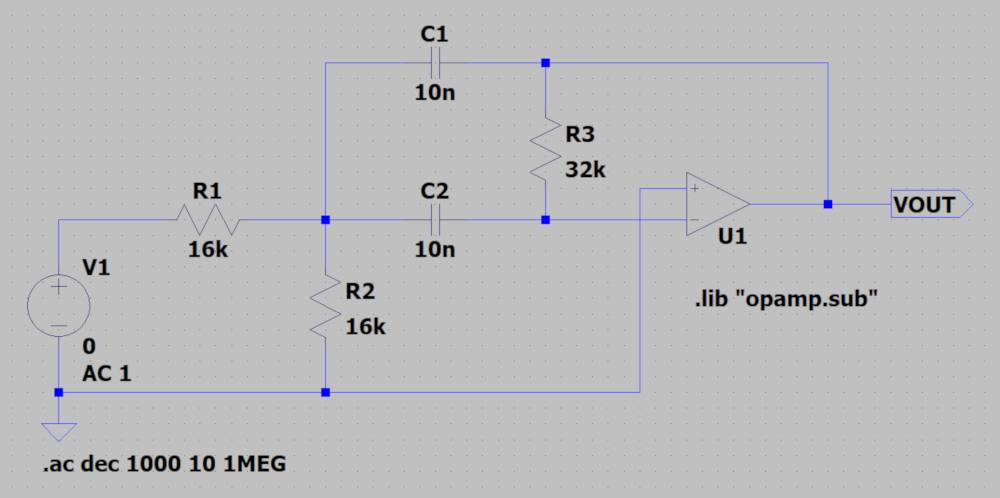
多重帰還型のバンドパスフィルタはこのような回路です。
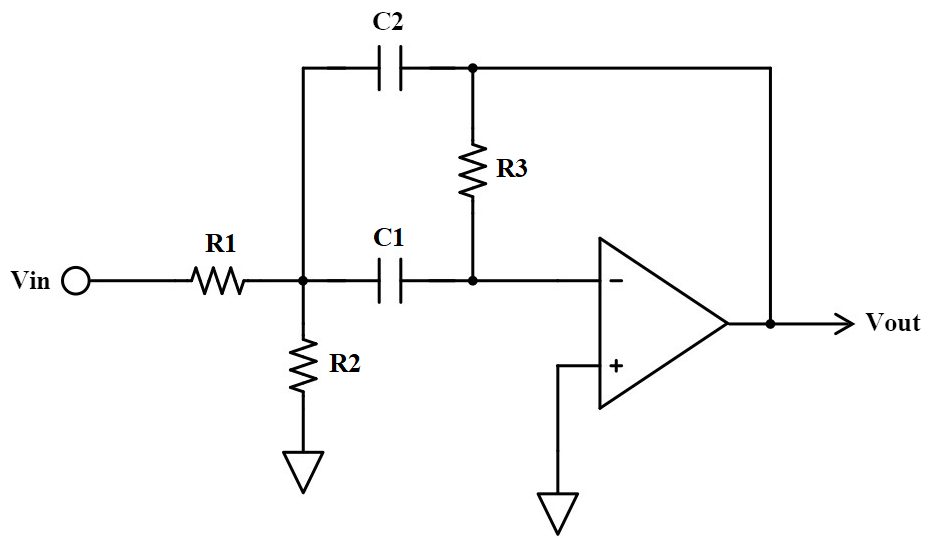
伝達関数、カットオフ周波数、Q値は以下の式で表されます。
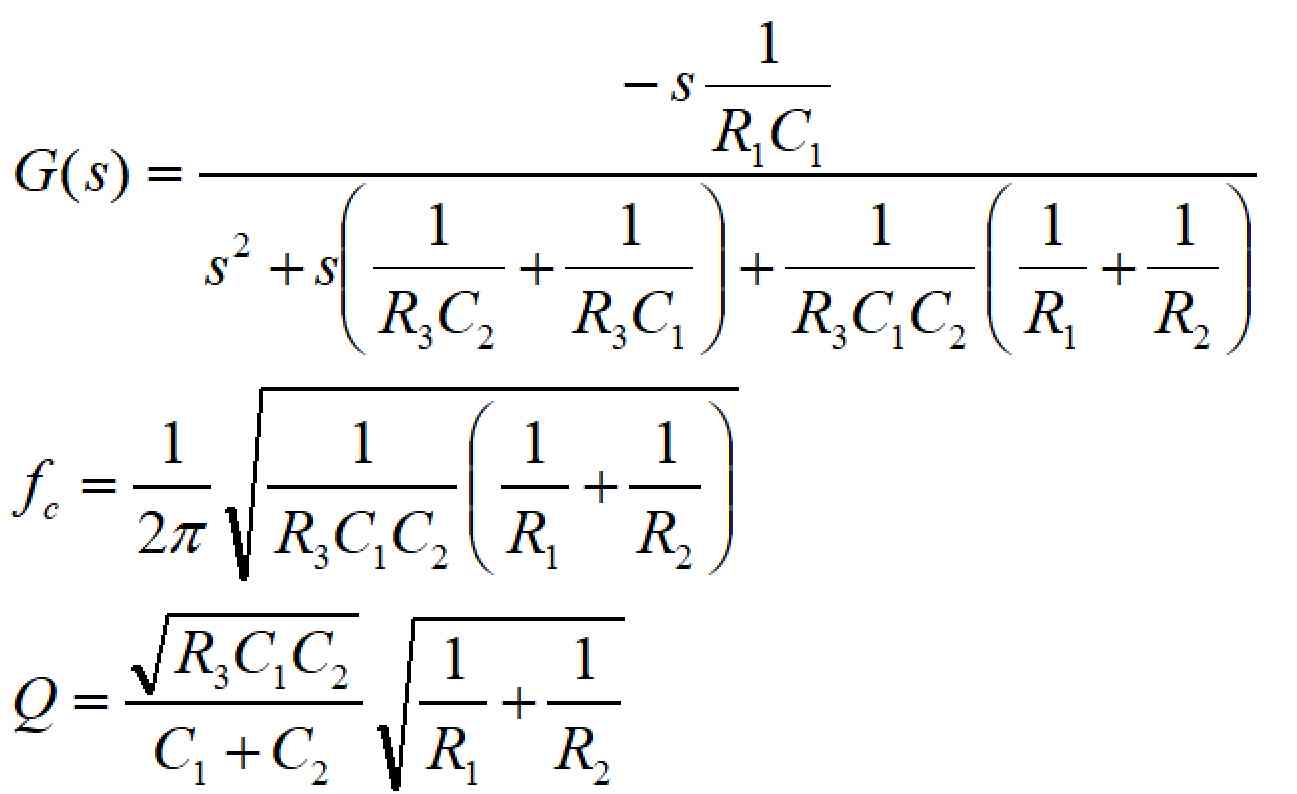
また、中心周波数でのゲイン:Kは
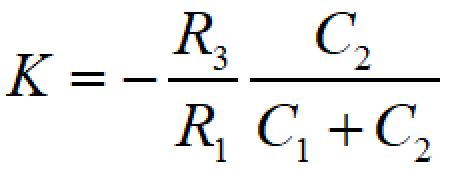
で表されます。
設計計算
計算を簡単にするため、C1=C2=C、R1=R2=R、Q=1とすると、
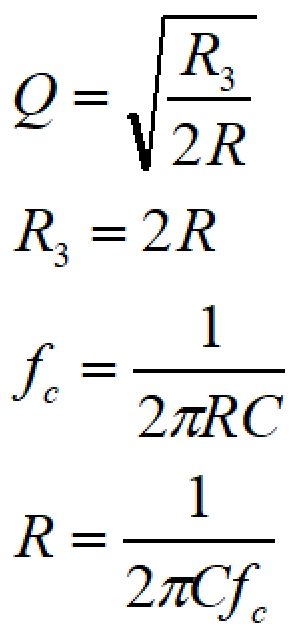
となります。
C=10nF、fc=1kHzとすると、
R1=R2=16kΩ、R3=32kΩと計算できます。
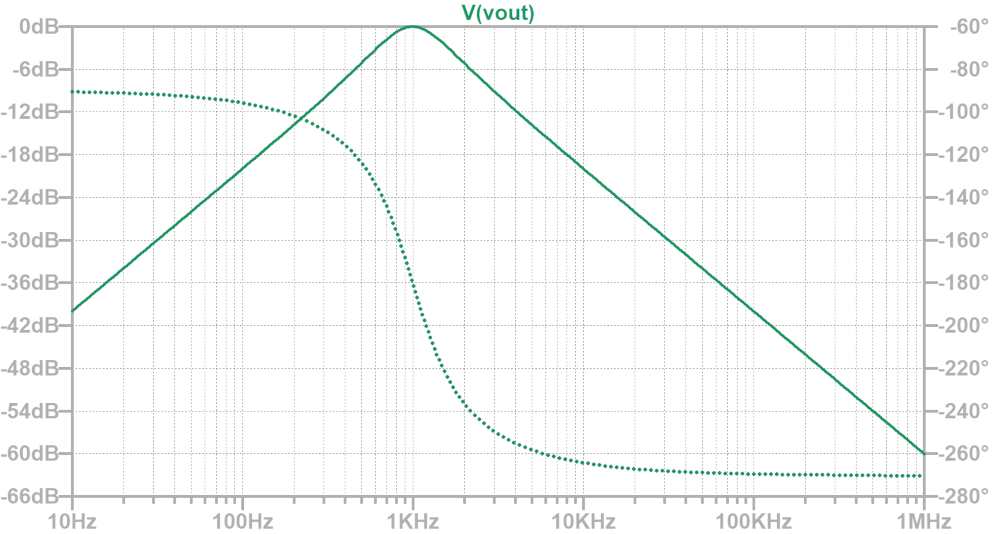
周波数特性
上記定数の周波数特性をLTspiceで確認すると以下のようになります。