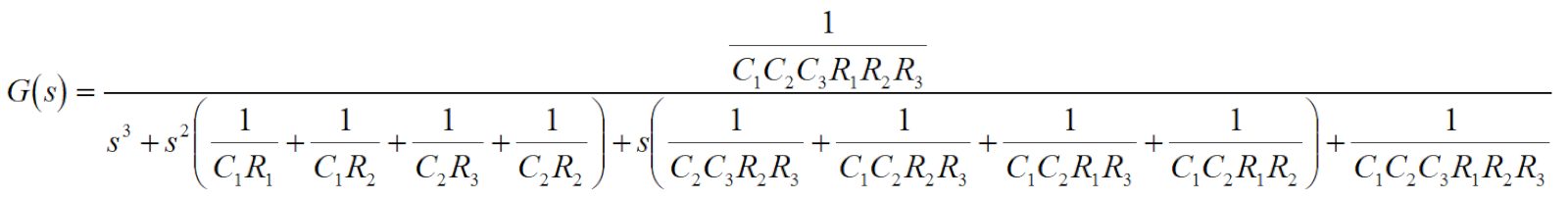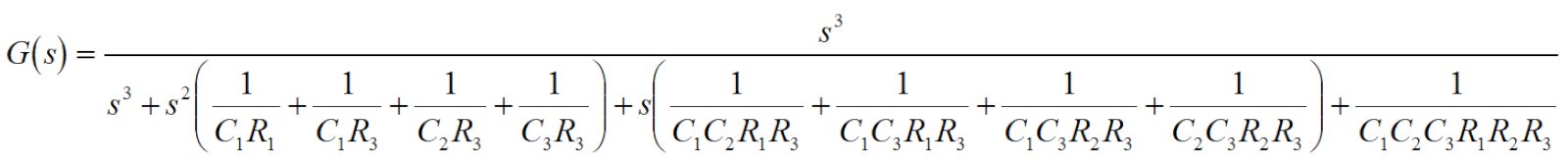サレンキー型3次フィルタの特性と設計計算
前回はサレンキー型2次フィルタについて解説しましたので、本稿ではサレンキー型の3次ローパスフィルタ、ハイパスフィルタの設計方法や特性について解説していきます。
3次ローパスフィルタ(LPF)
サレンキー型の3次ローパスフィルタはこのような回路です。
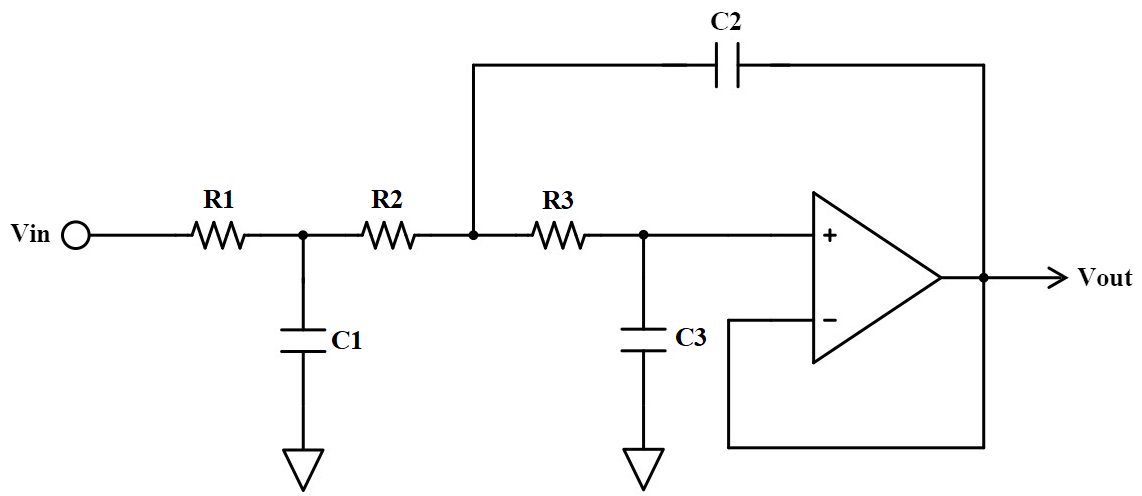
1次フィルタの後ろに2次のアクティブフィルタが接続された形になります。
伝達関数は以下の式で表されます。
設計計算
R1<<R2=R3とすることで、1次フィルタと2次フィルタをほぼ分けて考えることができます。
ここでは、R1=1kΩ、R2=R3=100kΩとします。
一次フィルタは単純なRCフィルタなので、カットオフ周波数は
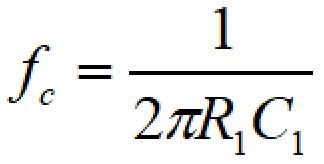
となります。
カットオフ周波数を1kHzとすると、C1=0.159uFとなります。
2次フィルタは前回の記事で解説した通り下記の式でC2、C3を求めることができます。
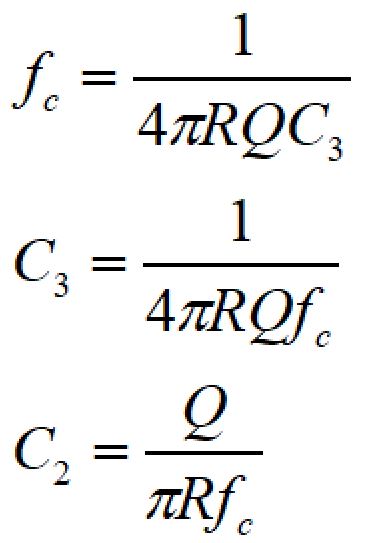
カットオフ周波数を1kHz、Q値を1とすると、C2、C3はC2=3183pF、C3=796pFとなります。
全体でのQ値は掛け算となり、1次フィルタのQ値が1/√2、2次フィルタが1なので、Q=0.707となります。
周波数特性
上記で求めた定数に近いものをE24系列から選んで、C1=0.16uF、C2=3300pF、C3=820pFとしてシミュレーションで周波数特性を確認します。
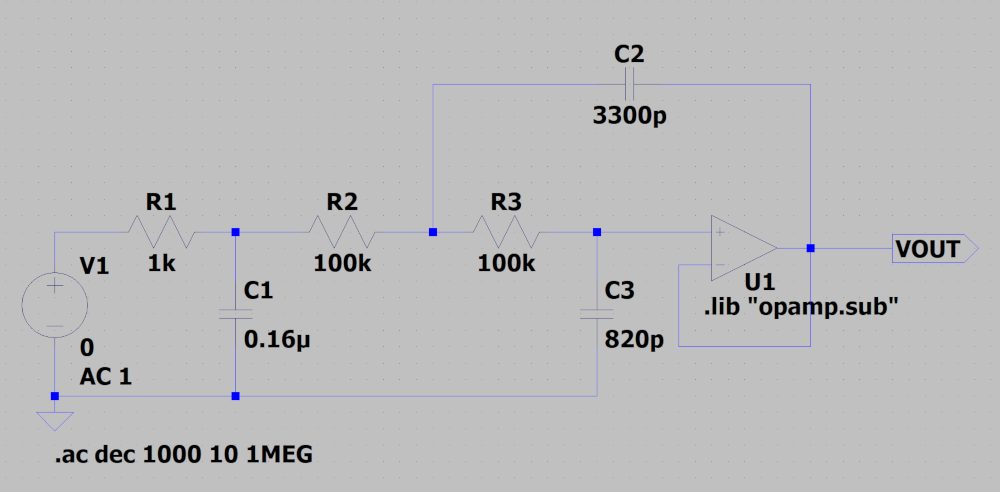
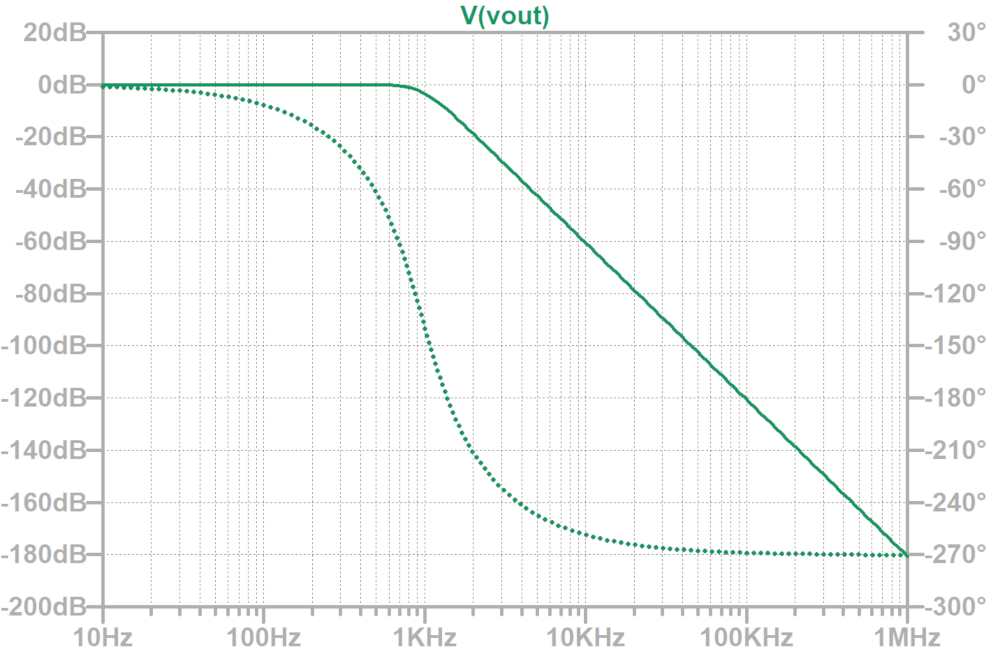
Q=0.707なので、カットオフ周波数で-3dBとなっています。
また、減衰特性は-60dB/decadeとなっています。
3次ハイパスフィルタ(HPF)
サレンキー型の3次ハイパスフィルタはこのような回路です。
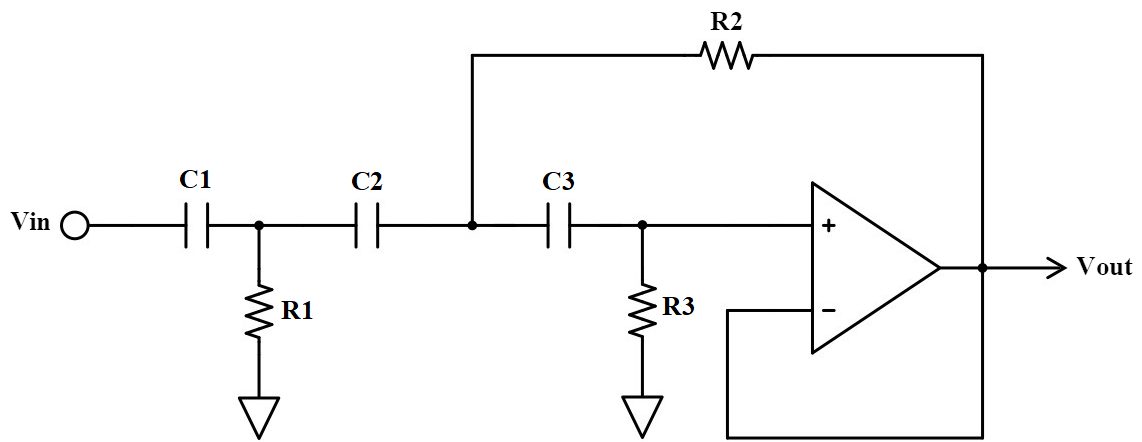
1次のハイパスフィルタの後ろに2次のアクティブフィルタが接続された形になります。
伝達関数は以下の式で表されます。
設計計算
C1>>C2=C3とすることで、1次フィルタと2次フィルタをほぼ分けて考えることができます。
ここでは、C1=0.1uF、C2=C3=1000pFとします。
一次フィルタは単純なRCのハイパスフィルタなので、カットオフ周波数は
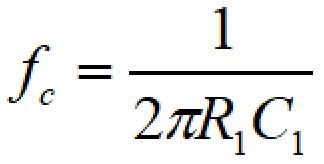
となります。
カットオフ周波数を1kHzとすると、R1=1.59kΩとなります。
2次フィルタは、下記の式でR2、R3を求めることができます。
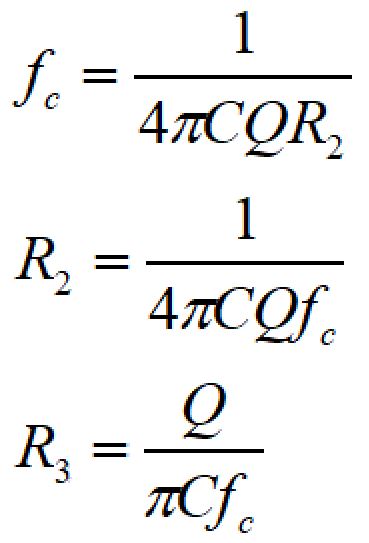
カットオフ周波数を1kHz、Q値を1とすると、R2、R3はR2=79.6kΩ、R3=318kΩとなります。
周波数特性
上記で求めた定数に近いものをE24系列から選んで、R1=1.6kΩ、R2=82kΩ、R3=330kΩとしてシミュレーションで周波数特性を確認します。
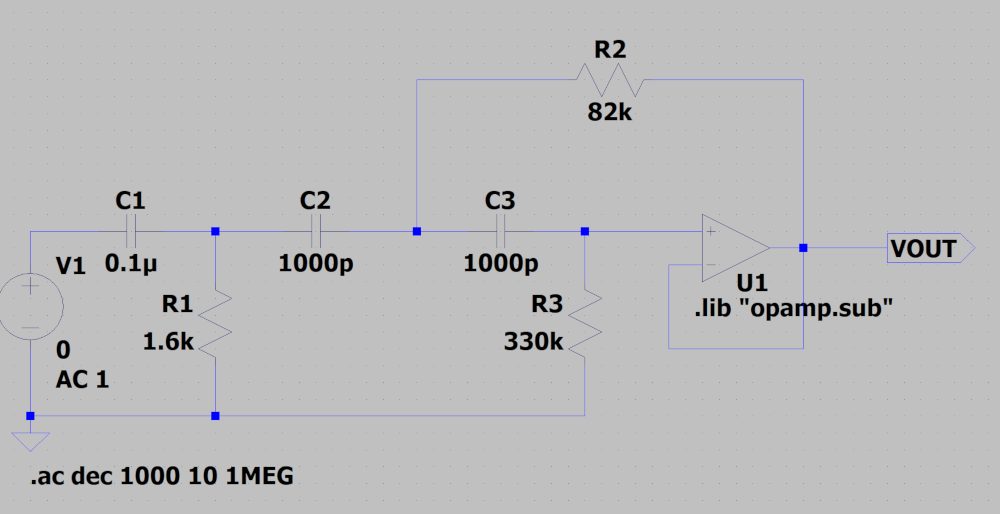
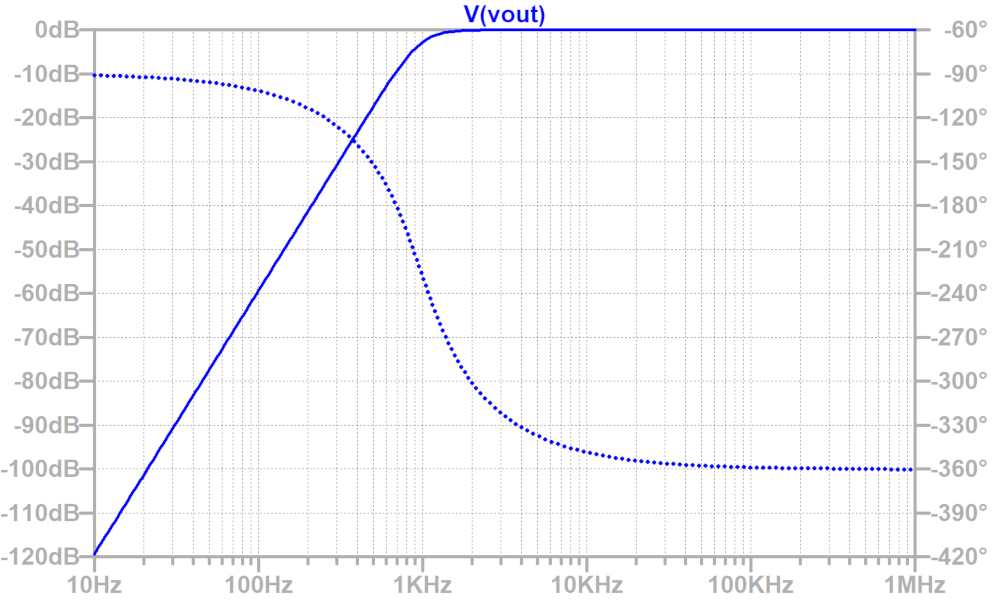
ローパスフィルタ同様、Q=0.707なので、カットオフ周波数で-3dBとなっています。
また、減衰特性は-60dB/decadeとなっています。