時定数とは？求め方や公式について解説

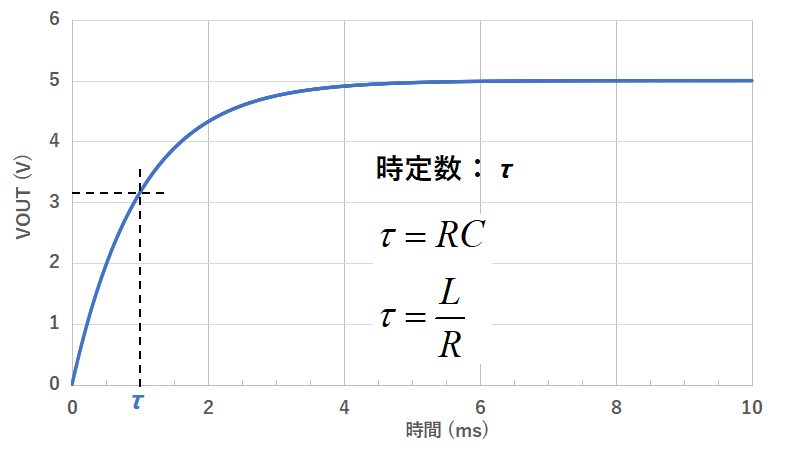
時定数とは、どのくらいの時間で平衡状態に達するかの目安で、電気回路における緩和時間のことを指します。
平衡状態の63.2%に達するまでの時間で定義され、時定数:τは、RC回路ではτ=RC、RL回路ではτ=L/Rで計算されます。

これだけだと少し分かりにくいので、計算式やグラフを用いて分かりやすく解説していきます。

RC回路の時定数

下図のRC回路を考えます。

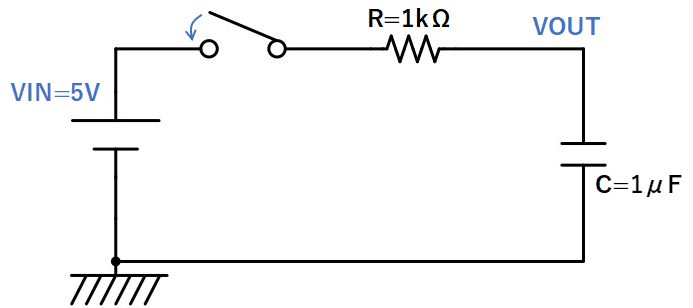
スイッチをオンすると、コンデンサに電荷が溜まっていき、VOUTは徐々にVINに近づきます。

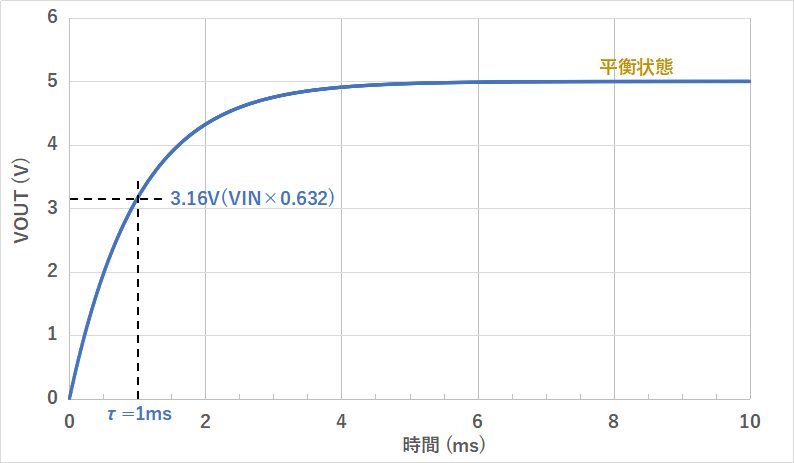
VOUT=VINの状態を平衡状態と呼び、平衡状態の63.2%、つまり、VOUT=0.632×VINになるまでの時間を時定数と呼びます。
時定数は記号:τ（タウ）で、単位はs（時間）です。

RC回路におけるコンデンサの充電電圧は以下の公式で表されます。

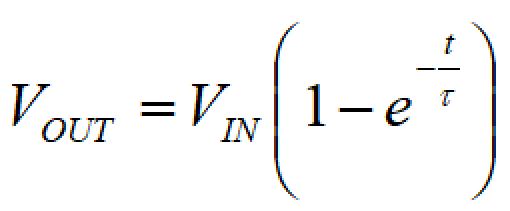
RC回路の場合、τ=RCとなるので、

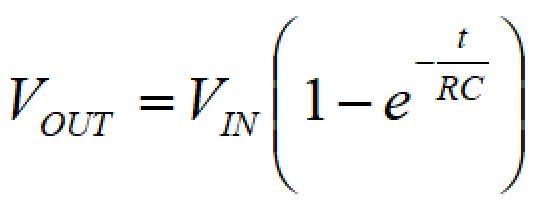
時間:t=τのときの電圧を計算すると、

eは自然対数で、e=2.71828… なので、

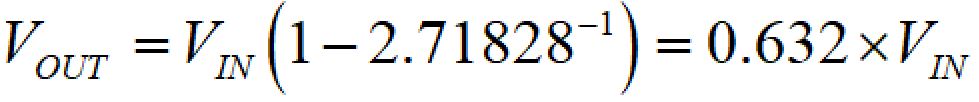
tが時定数に達したときに、電圧が平衡状態の63.2%になることが分かります。

時定数の導出

時定数は、コンデンサ充電電圧波形の、t=0における切線と平衡状態の電圧が交わる時間から導出されます。

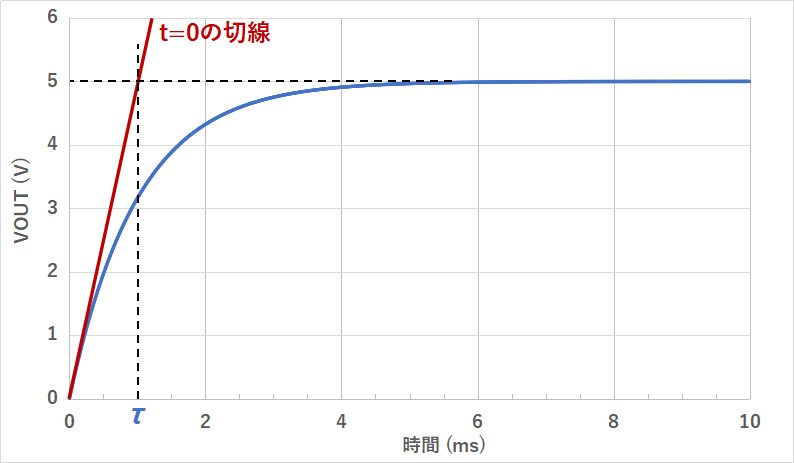
コンデンサ充電電圧の式を微分して計算してもいいのですが、電気回路的な視点から考えてみましょう。

t=0での電圧の傾きを考えていることから、t=0での電流でコンデンサを充電し続けた場合、何秒で平衡電圧に達するかを考えることと同じになります。

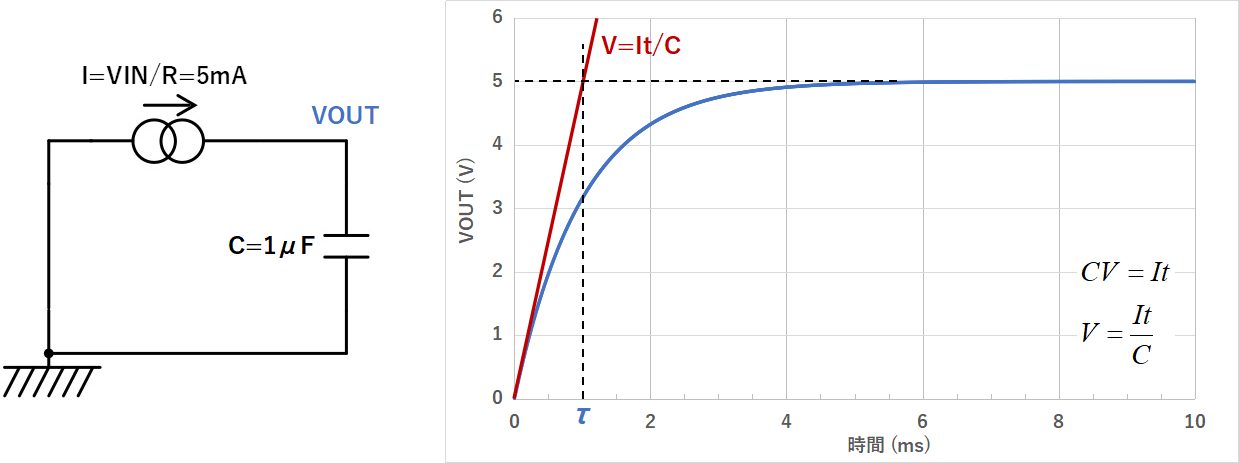
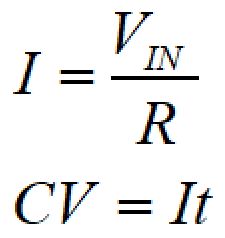
より

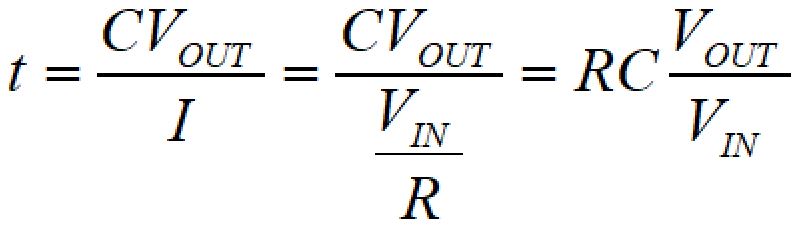
VOUT=VINとなる時間がτとなることから、

となり、τ=RCであることが導出されます。

充電完了までの目安

時定数の何倍の時間で、コンデンサの充電が何％進むかを覚えておけば、充電時間の目安を知ることができます。
先述の計算式

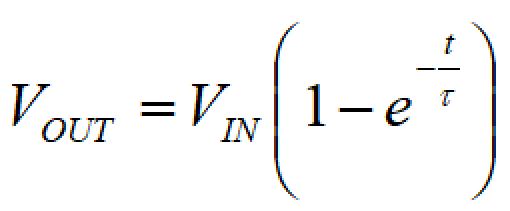
に、t=3τ、5τ、10τを代入すると、

となり、5τもあれば、ほぼ平衡状態に達することが分かります。

放電回路

今度は、コンデンサが平衡状態まで充電された状態から、抵抗をGNDに接続して放電されるまでの時間を考えます。

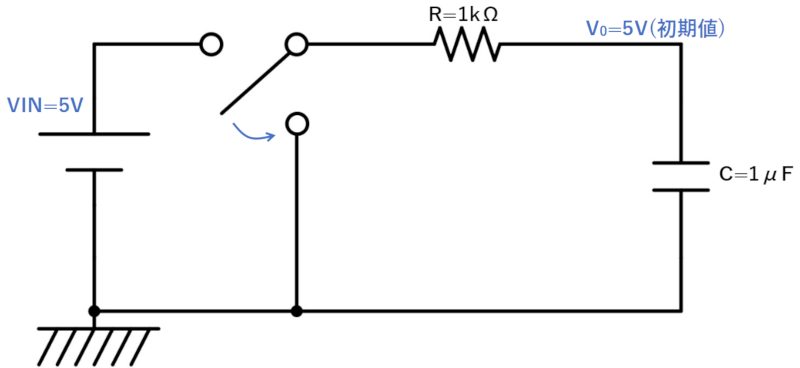
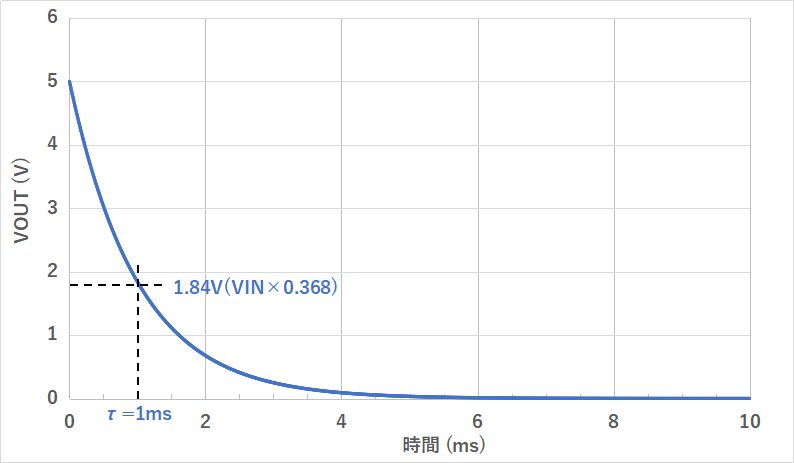
放電時のコンデンサの充電電圧は以下の式で表されます。

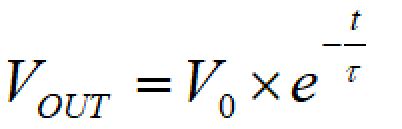
V0はコンデンサの電圧:VOUTの初期値です。
時間:t=τのときの電圧を計算すると、

tが時定数に達したときに、電圧が初期電圧の36.8%になることが分かります。

RL回路の時定数

下図のRL回路を考えます。

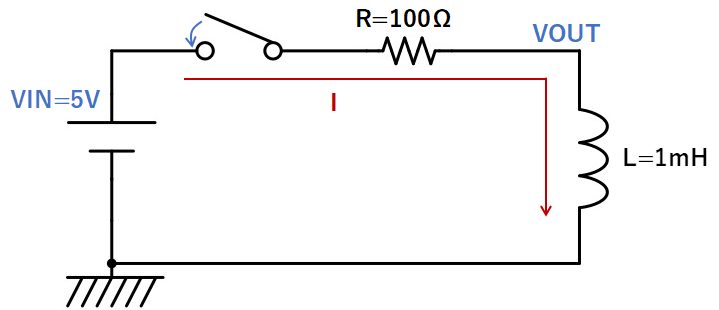
スイッチをオンすると、コイルに流れる電流が徐々に大きくなっていき、VIN/Rに近づきます。
I=VIN/Rの状態が平衡状態で、平衡状態の63.2%の電流に達するまでの時間が時定数となります。

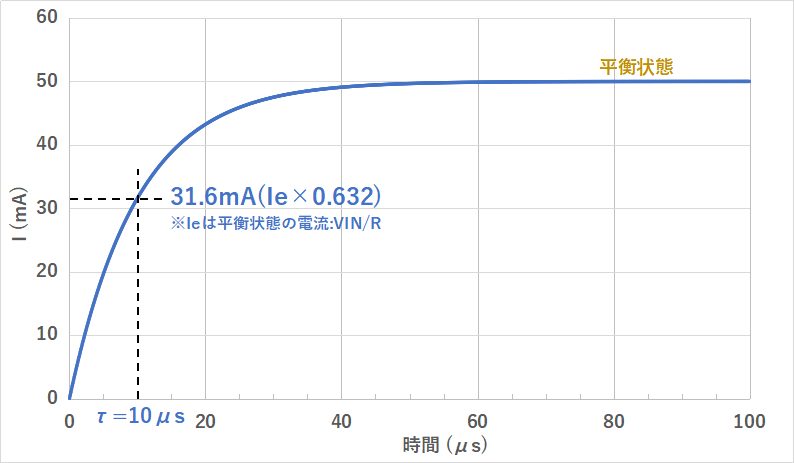
RL回路におけるコイル電流は以下の公式で表されます。

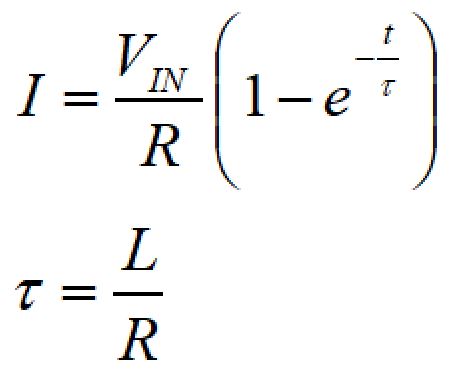
時定数の導出

RL回路の時定数は、コイル電流波形の、t=0における切線と平衡状態の電流が交わる時間から導出されます。

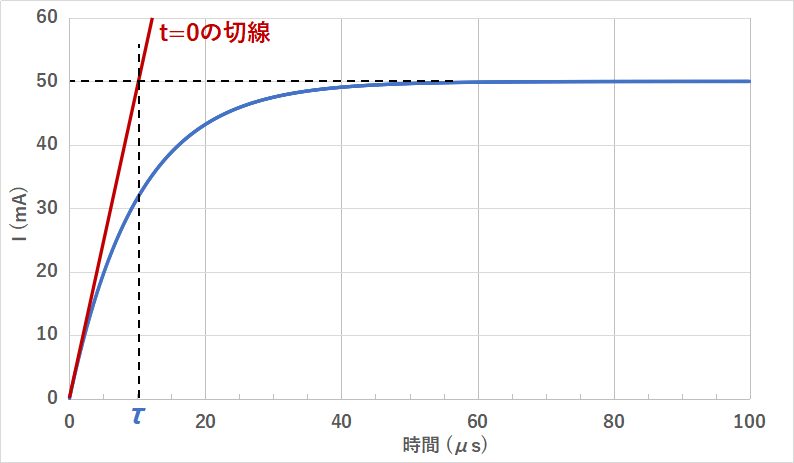
コイル電流の式を微分して計算してもいいのですが、電気回路的な視点から考えてみましょう。
t=0での電流の傾きを考えていることから、t=0での電圧をコイルに印加し続けた場合、何秒で平衡電流に達するかを考えることと同じになります。

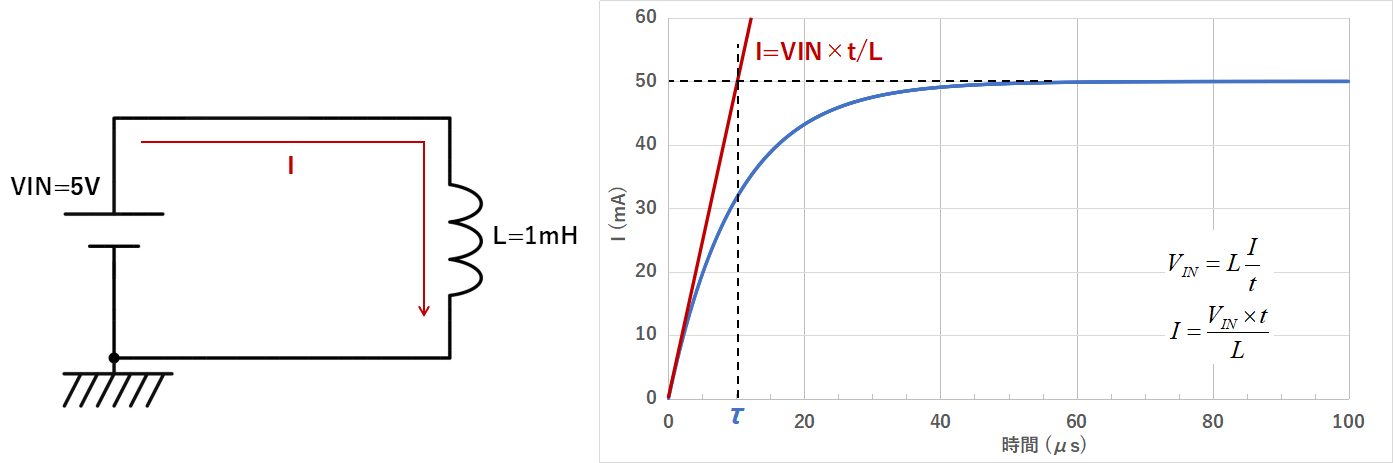
コイルに一定電圧を印加し続けた場合の関係式は、

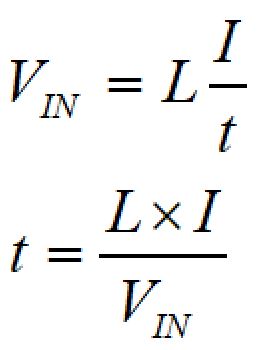
平衡状態の電流：Ieは

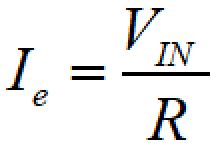
よって、平衡状態の電流：Ieに達するまでの時間は、

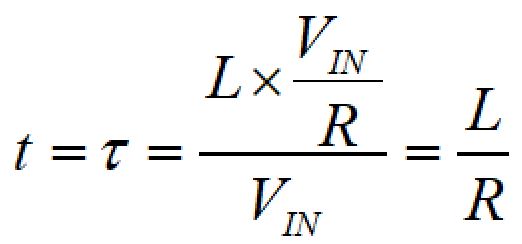
となり、τ=L/Rであることが導出されます。