カットオフ周波数の求め方

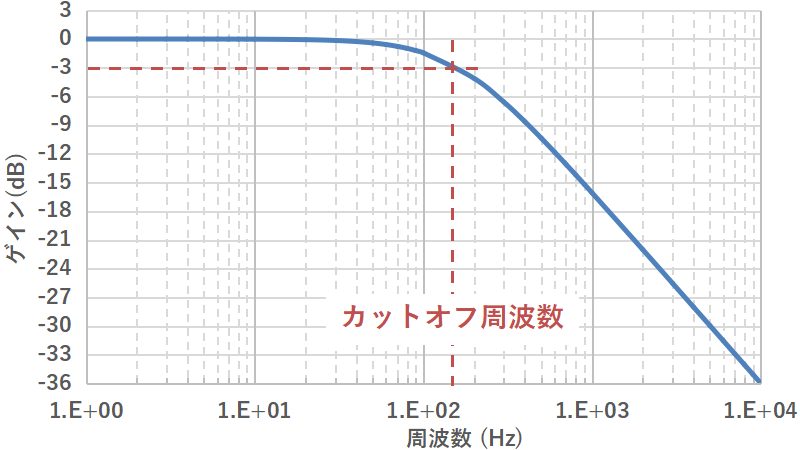
カットオフ周波数とは、フィルタ回路において入力信号がそのまま通過する帯域と、減衰される帯域の境目の周波数のことで、ゲインが3dB下がった周波数で定義されます。
カットオフ周波数は、遮断周波数とも呼ばれます。

カットオフ周波数の計算方法

RCフィルタ、LCフィルタのカットオフ周波数の計算式、周波数特性について解説していきます。

RCフィルタ（一次遅れ系）

RCフィルタのカットオフ周波数：fcは次式で計算できます。

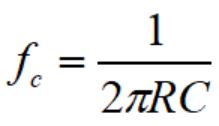
実際の回路を例に挙げカットオフ周波数を計算してみます。

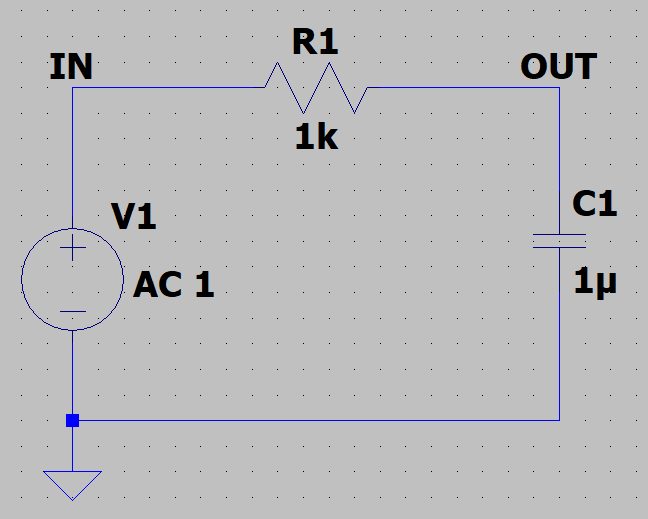
RCローパスフィルタ回路

R=1kΩ、C=1uFのローパスフィルタを考えます。

カットオフ周波数は、

fc = 1 / (2π × 1k ×1u) = 159Hz

と計算できます。
この回路の周波数特性は以下のようになります。

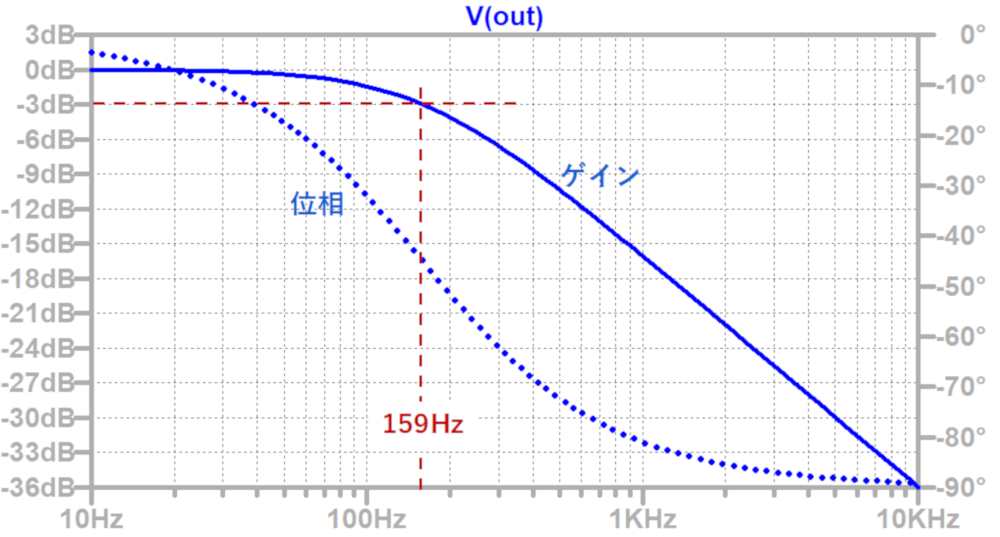
カットオフ周波数でゲインが3dB低下していることが分かります。
位相はカットオフ周波数で45°遅れ、全体では90°遅れます。

RCハイパスフィルタ回路

R=1kΩ、C=1uFのハイパスフィルタを考えます。

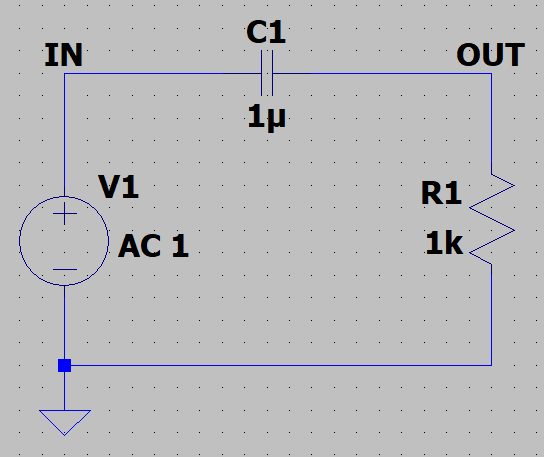
カットオフ周波数はローパスフィルタと同様で159Hzとなります。
この回路の周波数特性は以下のようになります。

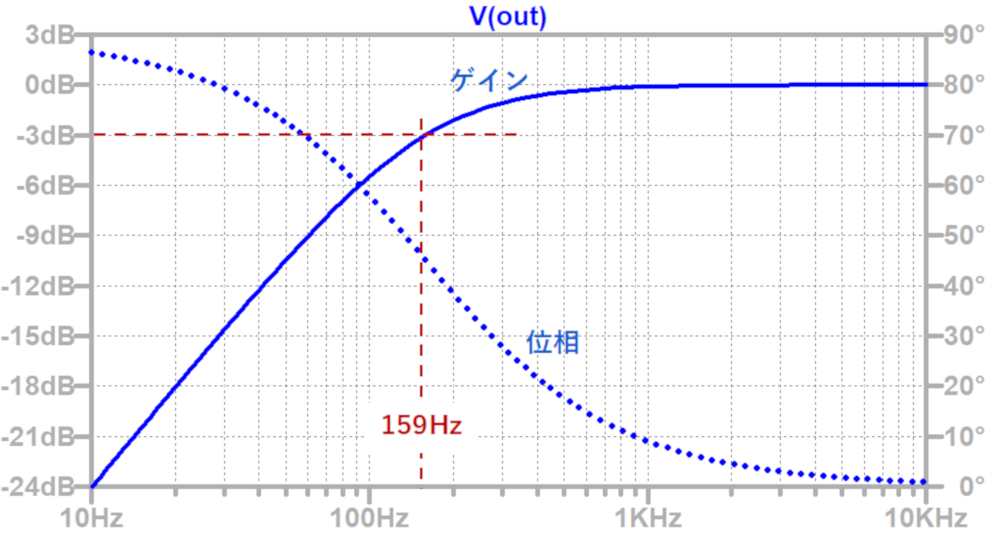
ゲインが-3dBになる周波数がカットオフ周波数です。
位相はカットオフ周波数で45°進み、全体では90°進みます。

RLフィルタ（一次遅れ系）

RLフィルタのカットオフ周波数：fcは次式で計算できます。

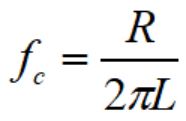
実際の回路を例に挙げカットオフ周波数を計算してみます。

RLローパスフィルタ

R=10Ω、L=100uHのローパスフィルタを考えます。

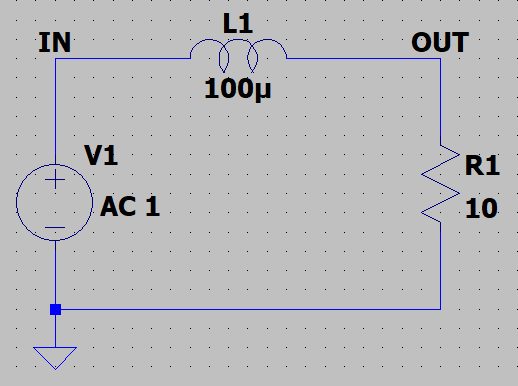
カットオフ周波数は、

fc = 10 / (2π × 100u) = 15.9kHz

と計算できます。
この回路の周波数特性は以下のようになります。

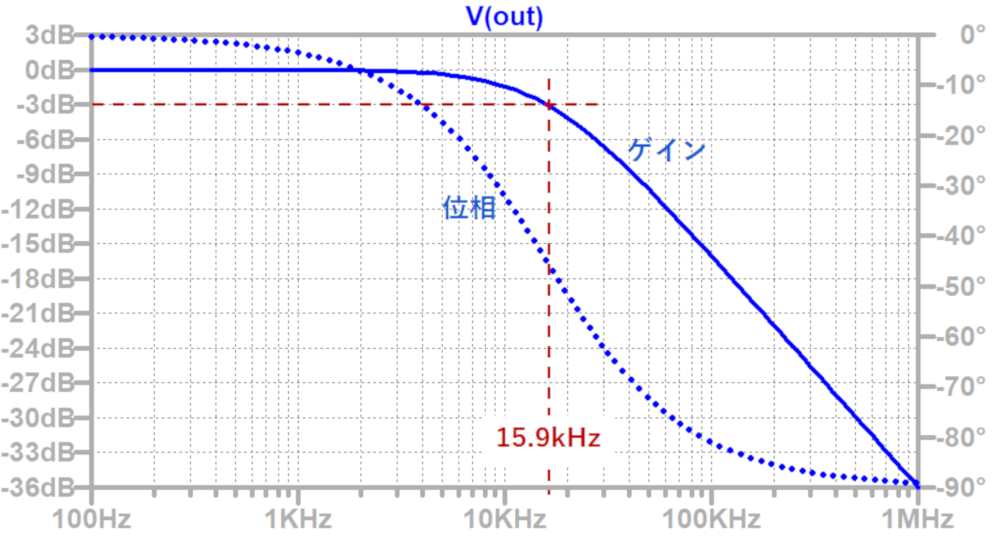
カットオフ周波数でゲインが3dB低下していることが分かります。
位相はカットオフ周波数で45°遅れ、全体では90°遅れます。

RLハイパスフィルタ回路

R=10Ω、L=100uHのハイパスフィルタを考えます。

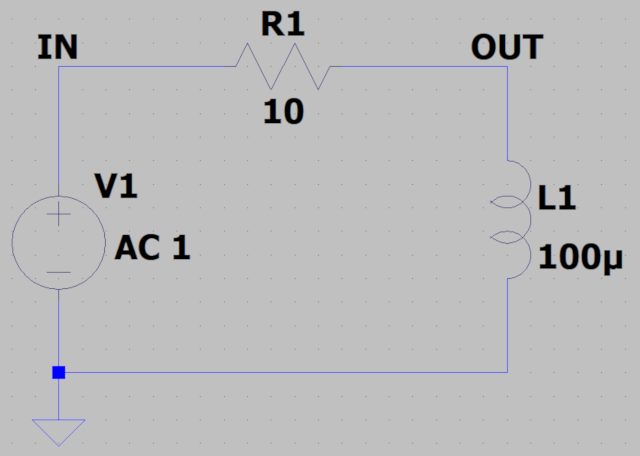
カットオフ周波数はローパスフィルタと同様で15.9kHzとなります。
この回路の周波数特性は以下のようになります。

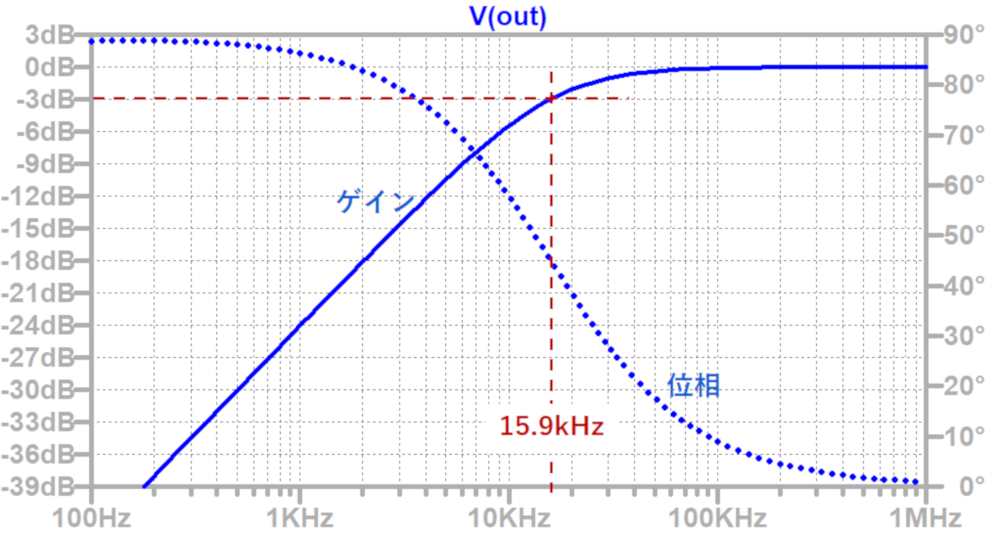
ゲインが-3dBになる周波数がカットオフ周波数です。
位相はカットオフ周波数で45°進み、全体では90°進みます。

LCフィルタ（二次遅れ系）

LCフィルタのカットオフ周波数は、LCの共振周波数で決まります。
カットオフ周波数：fcは次式で計算できます。

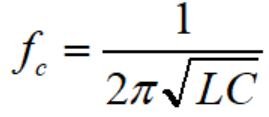
実際の回路を例に挙げカットオフ周波数を計算してみます。

LCローパスフィルタ

L=100uH、C=100uFのLCフィルタを考えます。
理想条件のLCフィルタの場合、共振周波数でのゲインのピークが無限大になってしまうため、コイルの等価直列抵抗として100mΩを想定します。

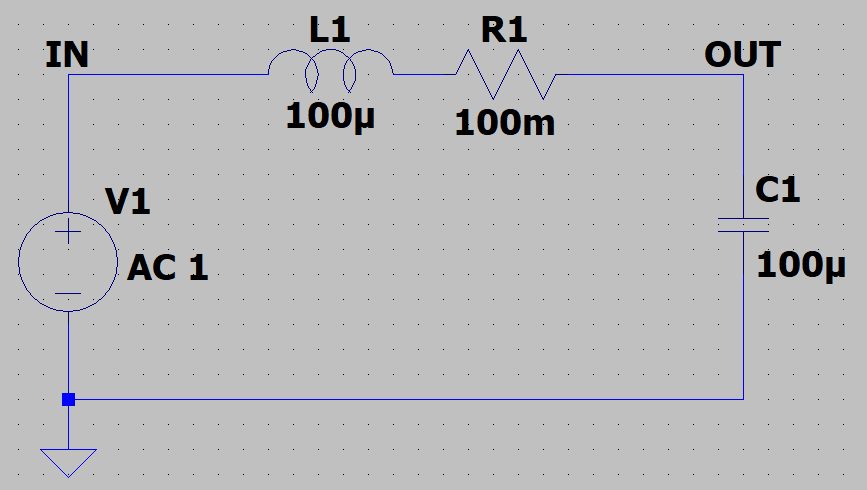
カットオフ周波数は、

fc = 1 / (2π × √(100u ×100u) ) = 1.59kHz

となります。
この回路の周波数特性は以下のようになります。

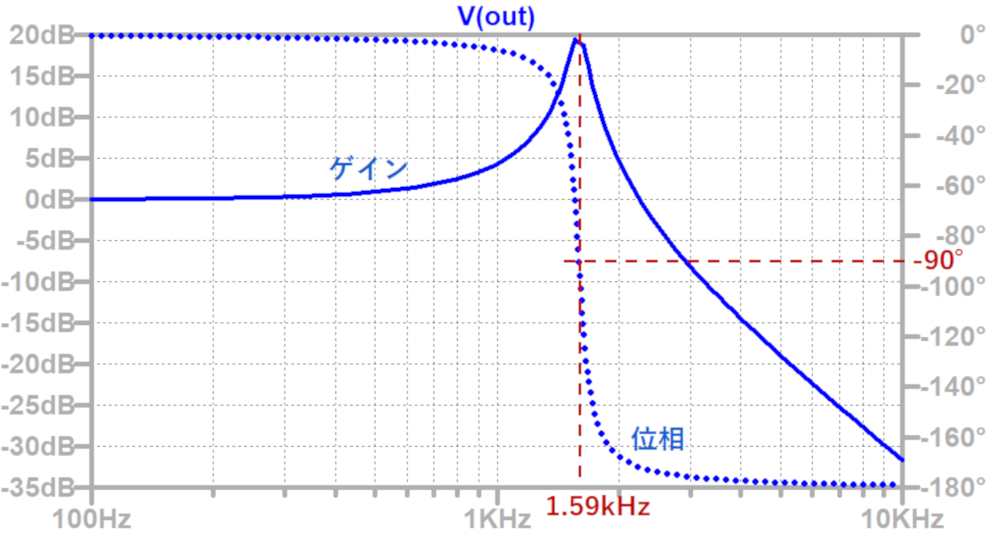
カットオフ周波数でゲインの盛り上がり（ピーク）が発生します。
Rの値が大きいほど、ピークが低くなり、ゲインの低下の傾きが緩くなります。

カットオフ周波数で位相が90°遅れ、全体では180°遅れます。

LCハイパスフィルタ

L=100uH、C=100uFのLCフィルタを考えます。
ローパスフィルタ同様、コイルの等価直列抵抗として100mΩを想定します。

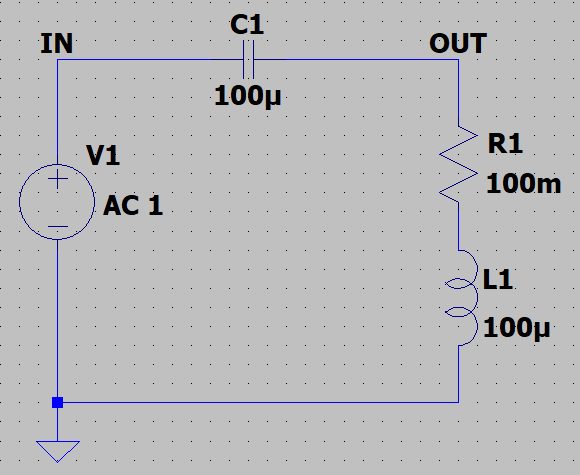
カットオフ周波数は1.59kHzとなります。
この回路の周波数特性は以下のようになります。

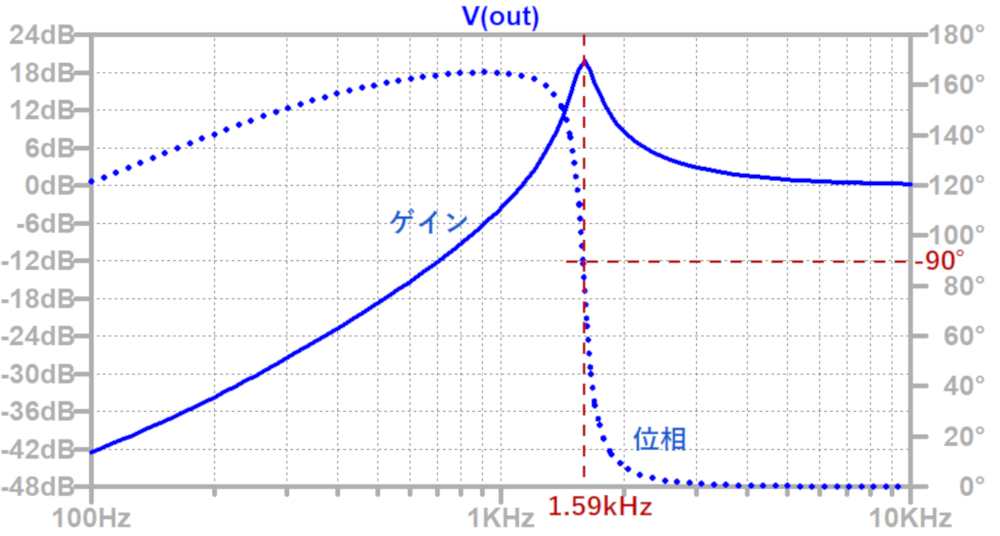
ローパスフィルタ同様、カットオフ周波数でピークが発生し、Rの値が大きいほどピークが低くなり、ゲインの傾きが緩くなります。

低周波領域では、RとLがハイパスフィルタとして働いています。
このRLハイパスフィルタのカットオフ周波数は、

fc = 100m / (2π × 100u) = 159Hz

となり、低域で位相が戻ってきているのはこのRLフィルタの影響です。