バンドパスフィルタ回路の原理と設計計算方法

バンドパスフィルタとは、特定の周波数帯域だけを通過させるフィルタです。
ローパスフィルタとハイパスフィルタを組み合わせたような構成で、目的の周波数以外を除去する用途で使われます。

本稿では、バンドパスフィルタの特徴・特性と計算方法などについて解説していきます。

バンドパスフィルタの回路図

バンドパスフィルタにはLCを並列にしたものと直列にしたものがあります。

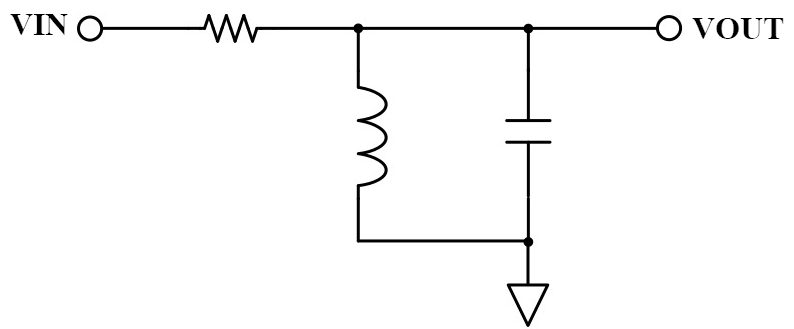
LC並列バンドパスフィルタ

LC並列の場合はRとCがローパスフィルタを構成し、RとLがハイパスフィルタを構成しています。

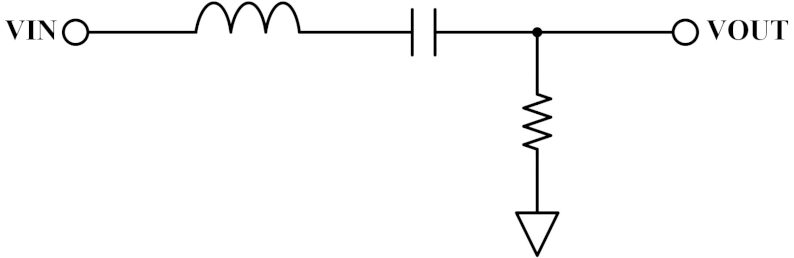
LC直列バンドパスフィルタ

LC直列の場合はRとCがハイパスフィルタを構成し、RとLがローパスフィルタを構成しています。

中心周波数、カットオフ周波数の計算

LC並列の場合の中心周波数、カットオフ周波数（遮断周波数）は次の式で表されます。

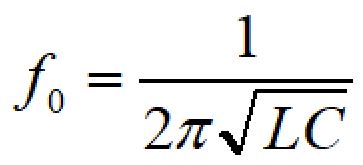
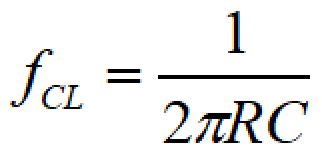
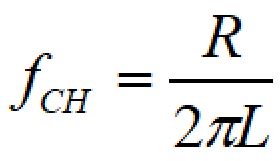
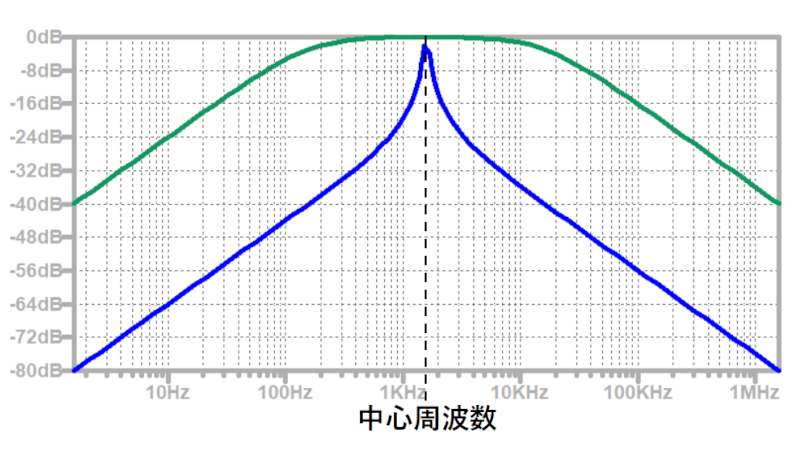
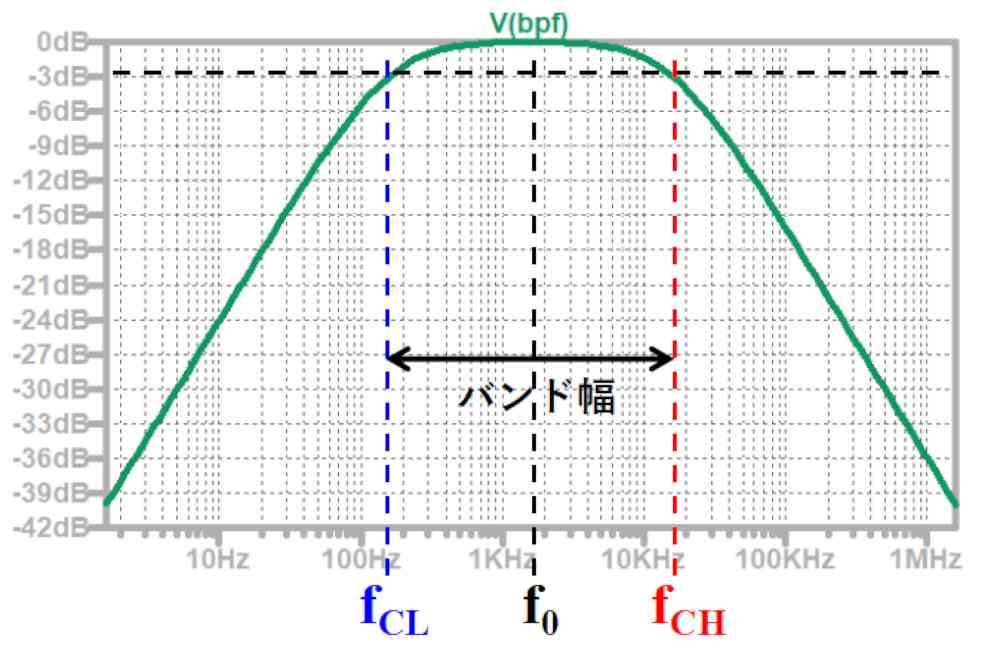
f0が中心周波数、fCLが低周波側カットオフ周波数、fCHが高周波側カットオフ周波数です。

周波数特性は以下のようになります。

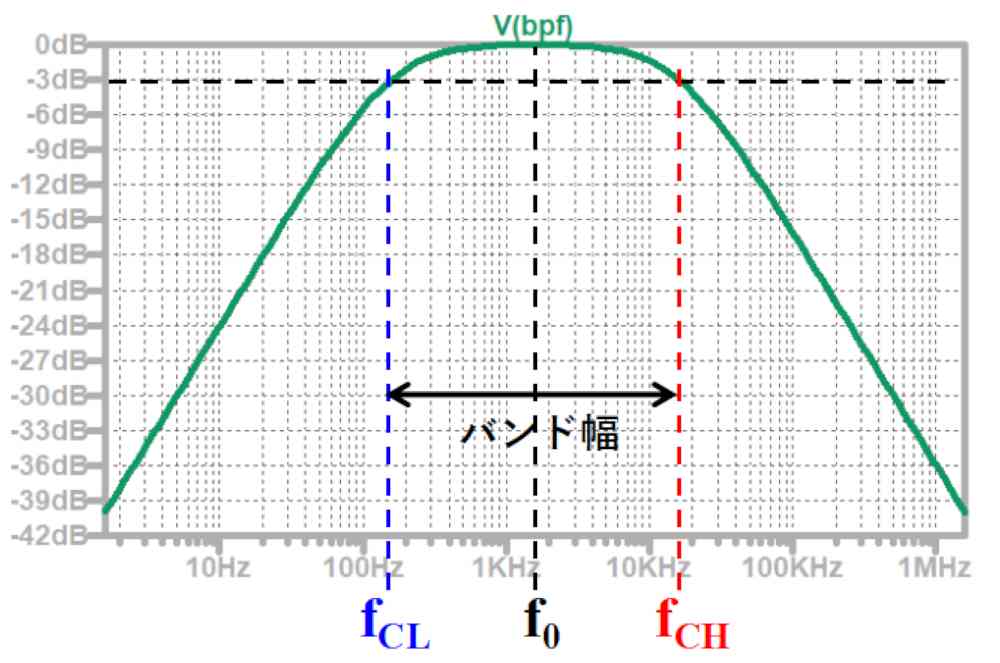
LC直列の場合の中心周波数、カットオフ周波数（遮断周波数）は次の式で表されます。

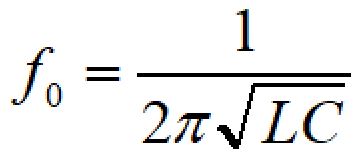
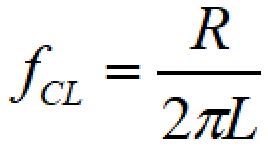
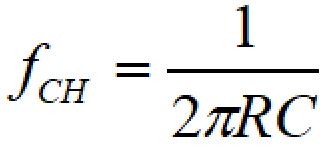
周波数特性は以下のようになります。

伝達関数

バンドパスフィルタの伝達関数は次の式で表されます。

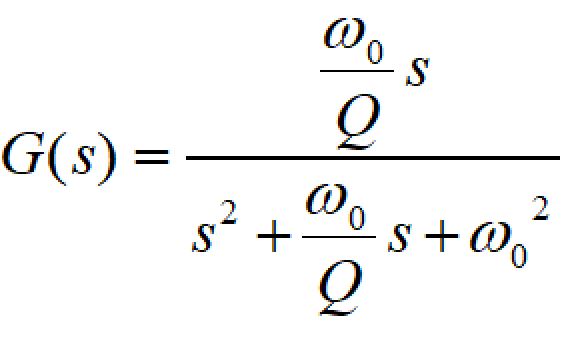
ω0は中心角周波数(rad/s)、Qはフィルタの鋭さを表すQ値と呼ばれる値です。

Q値の計算

Q値は次の式で計算できます。

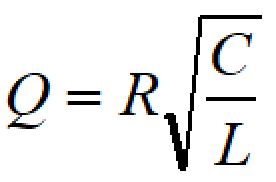
LC並列のQ値

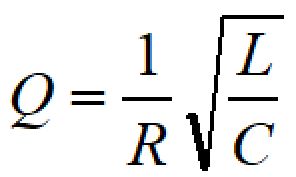
LC直列のQ値

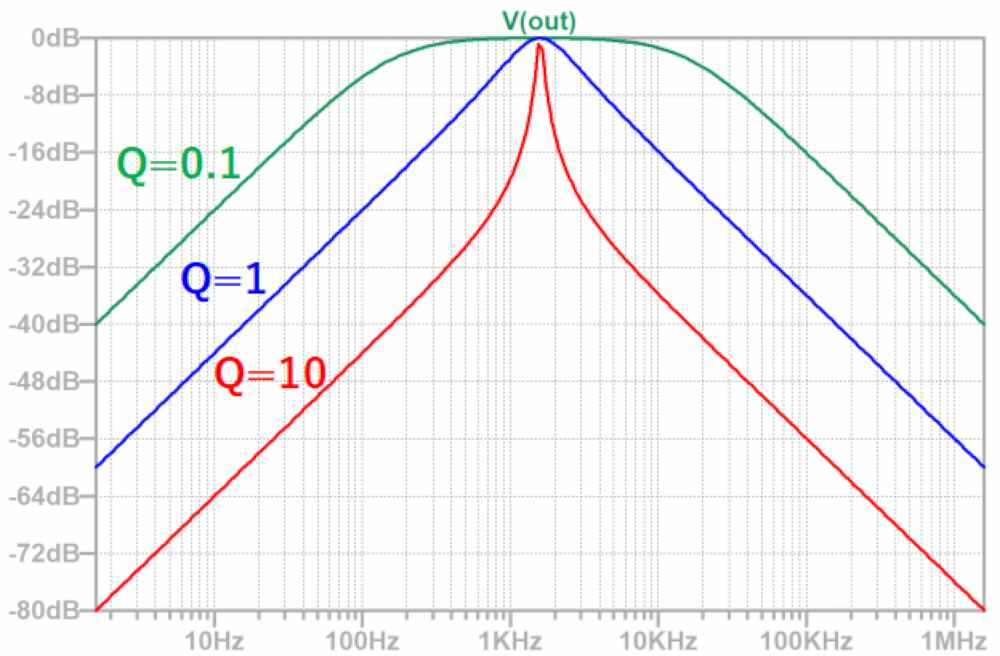
Q値によって以下のようにフィルタ特性が変化します。

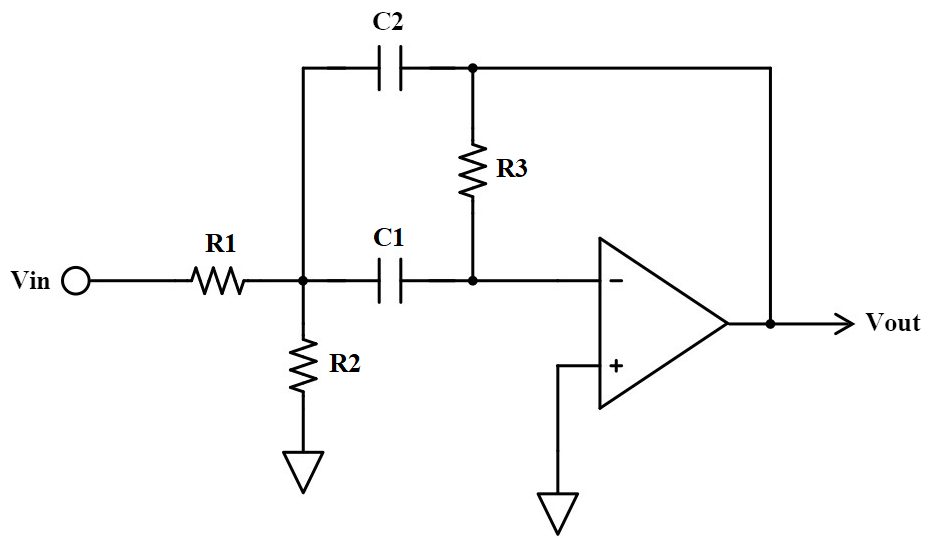
オペアンプを使ったバンドパスフィルタ

オペアンプを使ったフィルタはアクティブフィルタと呼ばれます。

詳細はこちらの記事をご参照ください。
オペアンプを使ったバンドパスフィルタ