スイッチングレギュレータの位相補償のやり方と位相余裕の計算方法
スイッチングレギュレータ(DCDCコンバータ)の位相余裕を計算するのはそれほど難しくはありません。
伝達関数を使うので少し取っ付きにくいイメージがありますが、コツさえつかめば簡単です。
計算用のエクセルシートもご用意しましたので、数値を変えながらボーデ線図の変化を確認すればイメージがつかみやすくなると思います。
電流モードと電圧モードで大きく考え方が異なりますので、2パターンに分けて解説していきます。
電流モードの位相補償と計算
下図のような降圧型の電流モードスイッチングレギュレータを考えます。
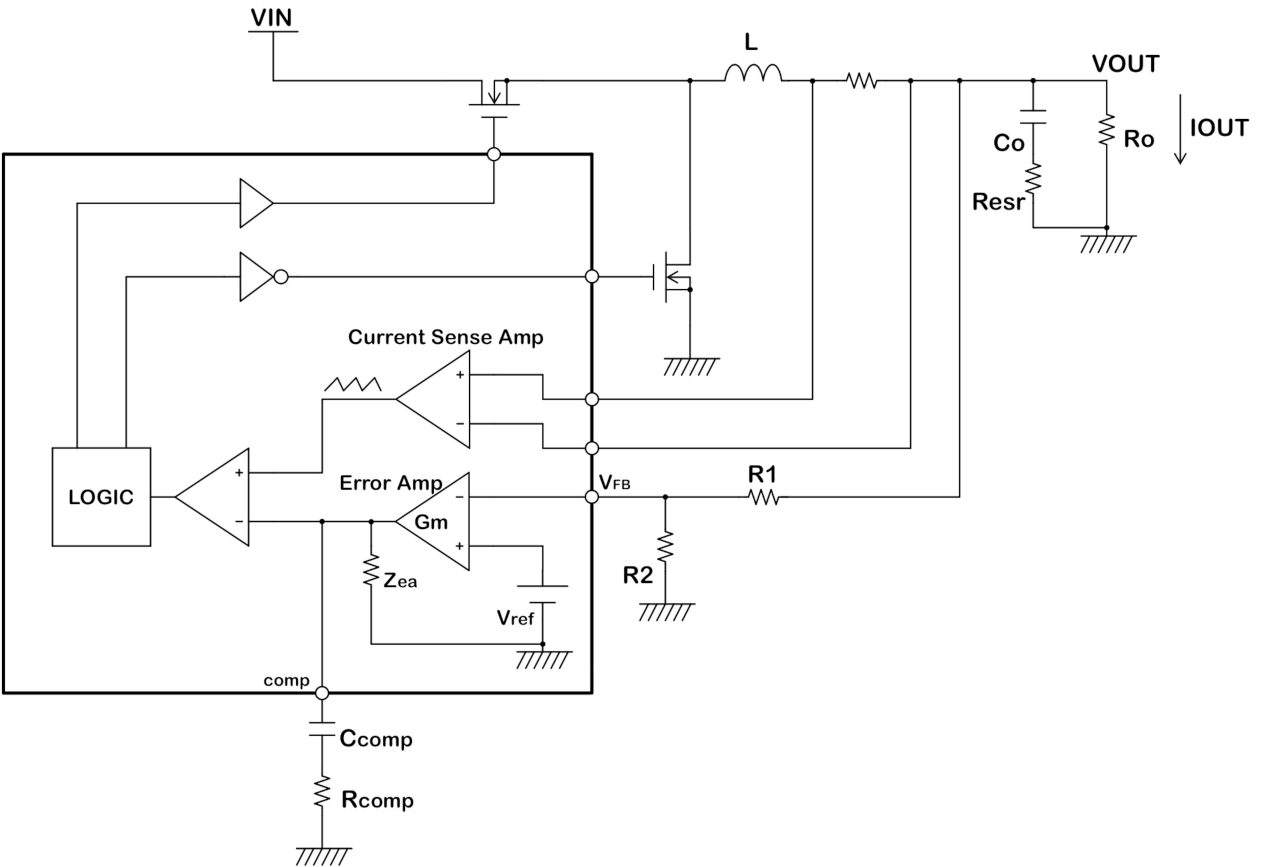
オープンループゲイン
はじめにレギュレータ全体のオープンループゲインを計算します。
VOUTを起点に一周するループを考えます。
まず、R1、R2による抵抗分割によるゲインは、
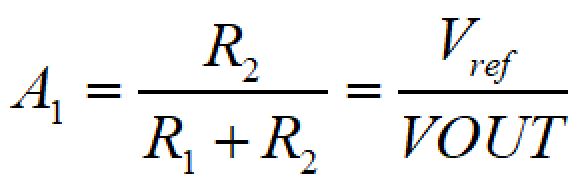
となります。
次にエラーアンプのゲインを考えます。
ICのデータシートに電圧増幅率の形で書かれている場合もありますし、トランスコンダクタンスと出力インピーダンスの形で書かれている場合もあります。
トランスコンダクタンス:gmeaと出力インピーダンス:Zeaを使ってゲインは、
で計算できます。
最後にエラーアンプの出力部からVOUTまでの増幅率を計算します。
comp端子からSW端子までの電流増幅率(単位:A/V)が規定されています。
電流センス抵抗が外付けの場合は、センス電圧と電流リミット値の関係から電流増幅率を計算することができます。
compからVOUTまでの増幅率A3は、
で計算できます。
gmpowerがcomp端子からSW端子までの電流増幅率、ROUTは負荷抵抗値です。
これらの積を取ることでオープンループゲインを計算することができます。
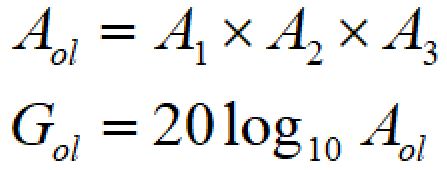
Golは増幅率をdBの単位に変換したものです。
簡単な位相補償の手順
電流モードの位相補償の手順は簡単で、
- SW周波数の1/10で0dBになるように1stポールを設定
- 出力コンデンサによるポールをゼロでキャンセル
だけです。
これにより、1stポールから20dB/decの傾きでゲインが低下し、SW周波数の1/10で0dBになります。
位相は90°だけ遅れますので、十分位相余裕が稼げます。
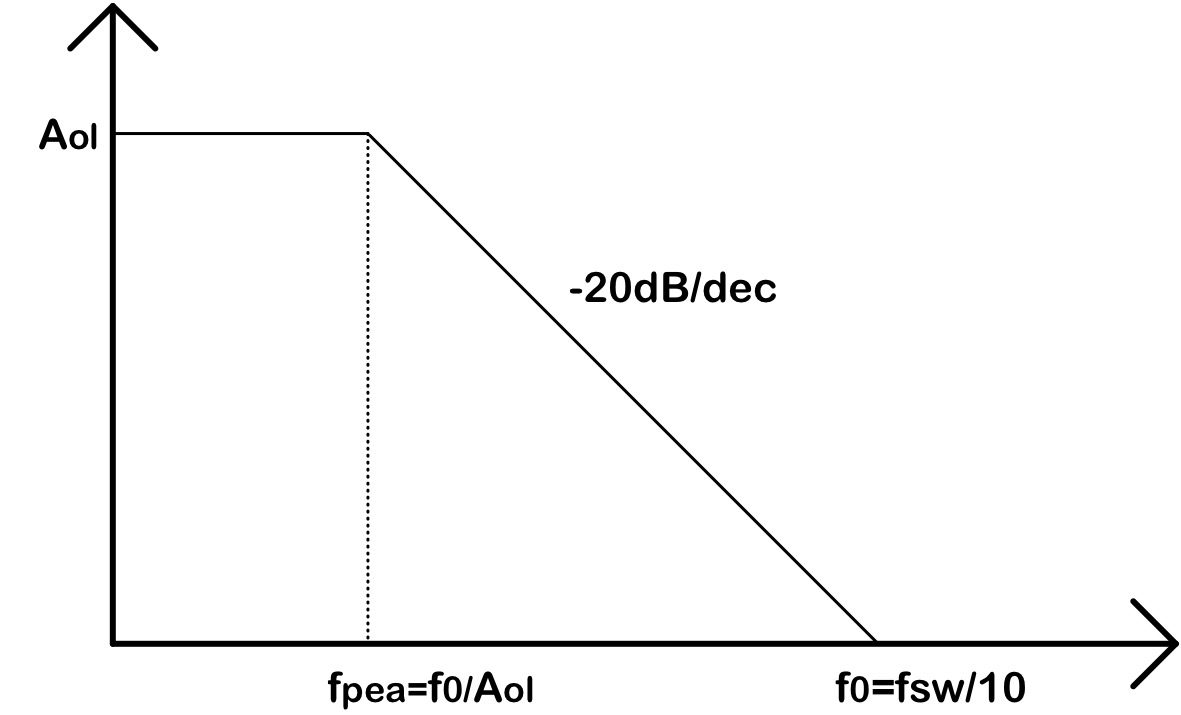
1stポールの設定
1stポール:fpeaはエラーアンプの出力に設置するコンデンサCcompにより設定します。
Ccompは以下の計算式から求めることができます。
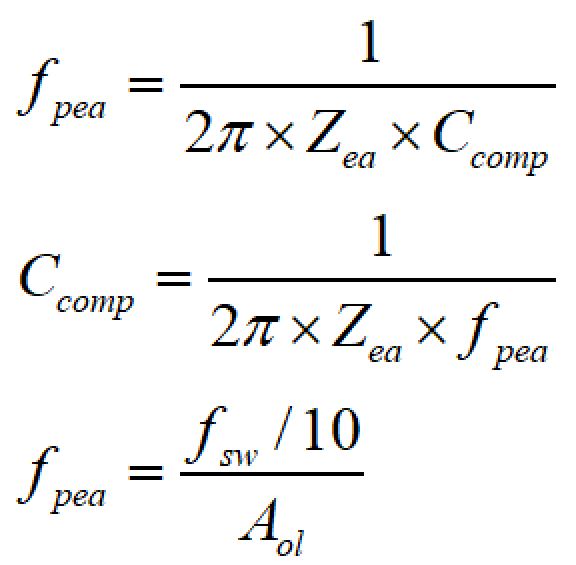
ゼロの設定
ゼロは出力コンデンサCoによってできるポールと同じ周波数に設定してポールをキャンセルします。
出力コンデンサによるポールの周波数は以下のように計算できます。
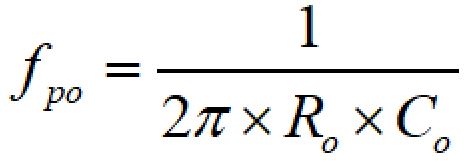
対するゼロは、エラーアンプ出力に設置した抵抗とコンデンサによって生成します。
ゼロの周波数は、
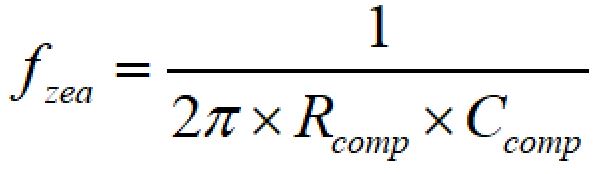
fpo = fzeaとするためのRcompは、
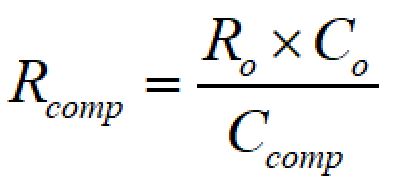
と計算できます。
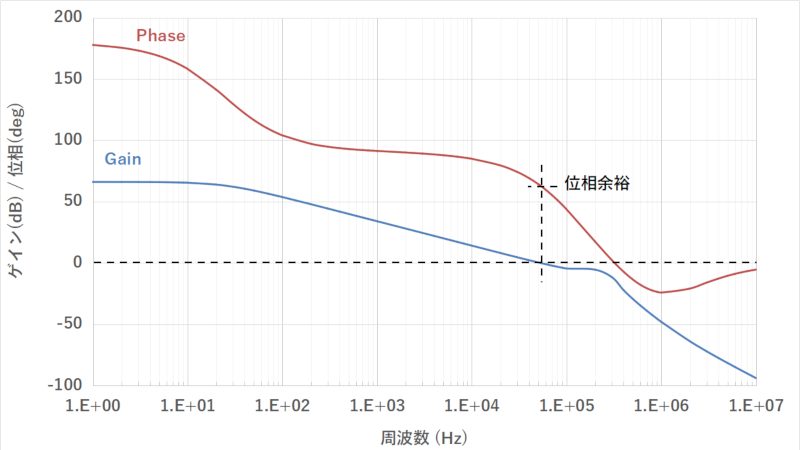
ボーデ線図は下記のようなイメージになります。
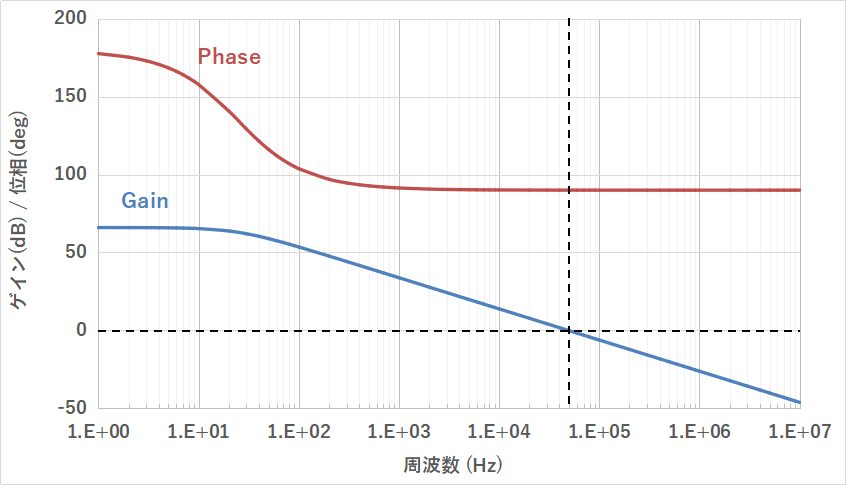
条件:VOUT=5V、Vref=0.8V、gmea=750uA/V、Zea=1.333MΩ、fsw=500kHz、gmpower=5A/V
これは簡易的なものですが、設計実務でも十分使える計算方法です。
実際の周波数特性は高周波側でダブルポールが発生するなど、もっと複雑なものになります。
伝達関数を計算すると、実際の動きに近い周波数特性を得ることができます。
伝達関数を計算して位相余裕度を計算する
今回もVOUTを起点に一周するループを考えます。
フィードバック部
コンデンサの設置はありませんので位相遅れ、位相進みはありません。
抵抗分割によるゲインだけを考えます。
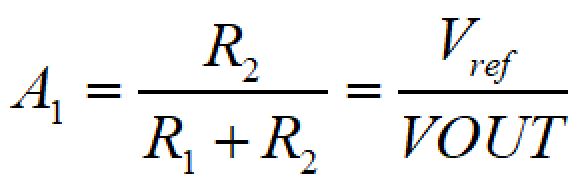
エラーアンプ部
エラーアンプの入力から出力までの伝達関数を考えます。
DCゲインはgmea×Zeaで計算できますが、Zeaと並列にCcompとRcompが設置されていますので、伝達関数としてはこれらを考慮に入れる必要があります。
エラーアンプの入力変動ΔVinに対する出力変動ΔVoutは以下の関係式で表すことができます。
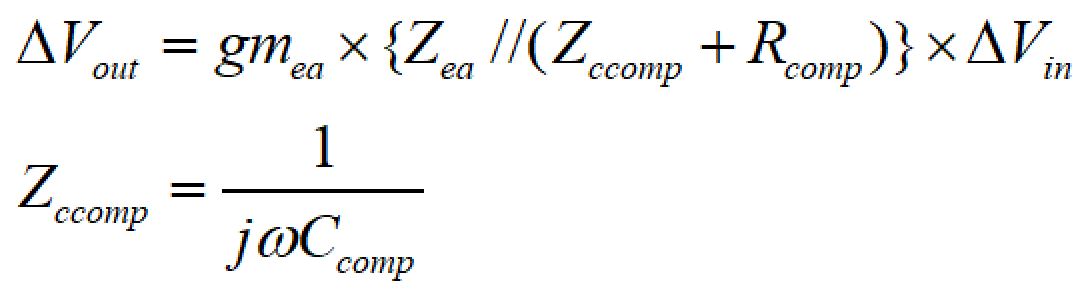
したがって、エラーアンプ部の伝達関数は、
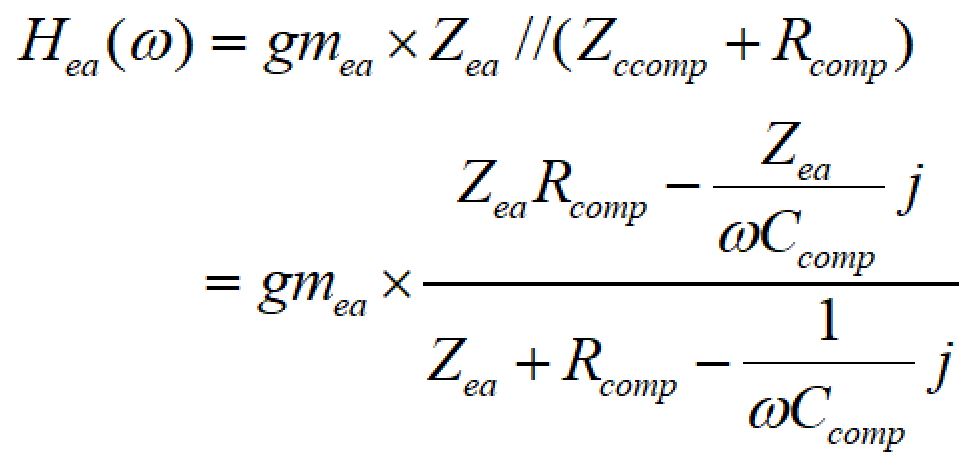
となります。
出力部
エラーアンプの出力部からVOUTまでの伝達関数を考えます。
エラーアンプの出力部の変動ΔVinに対する最終出力変動ΔVoutは以下の関係式で表すことができます。
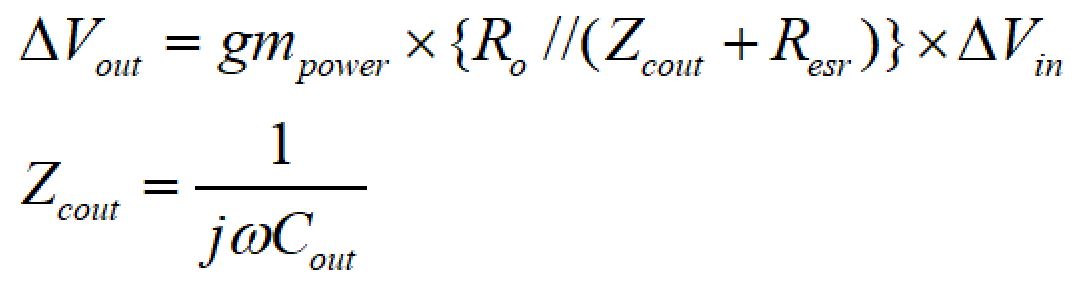
したがって、エラーアンプの出力部からVOUTまでの伝達関数は、
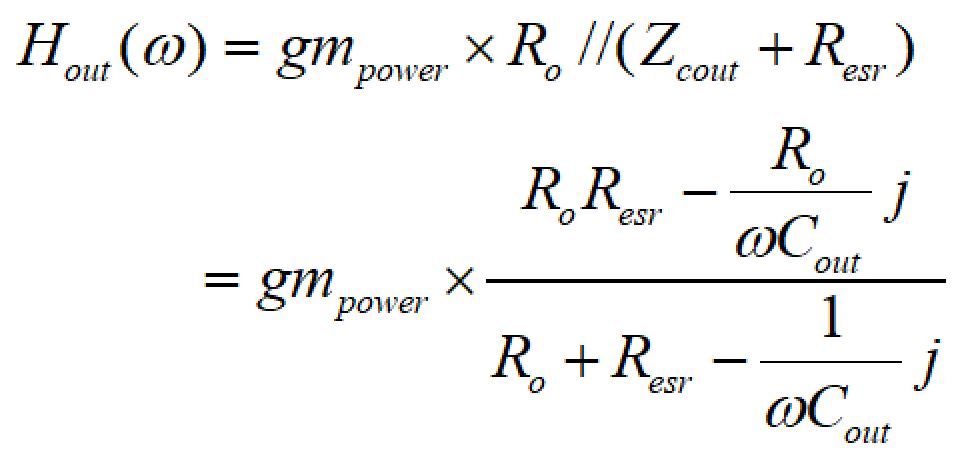
サンプリング・ポール
電流モードの場合、スイッチング周波数の1/2の周波数にダブルポールが発生します。
簡易計算でクロスオーバー周波数をスイッチング周波数の1/10としたのは、このサンプリング・ポールが発生するためです。
厳密に計算するためにはDUTYやスロープ補償が関わってきて複雑になるため、今回はQ値を固定した2次遅れ系の伝達関数を使います。
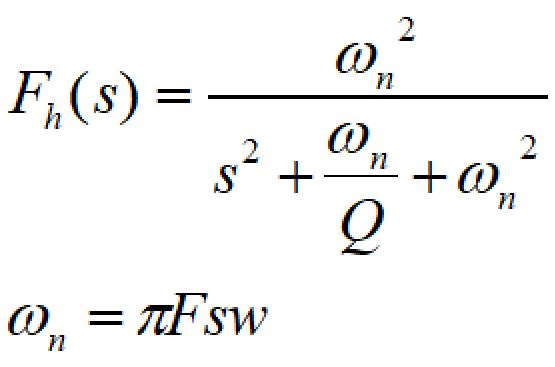
サンプリング・ポールの詳細の解説、計算方法については下記記事をご覧ください。
スロープ補償とは?DCDCコンバータのサブハーモニック発振を対策
レギュレータ全体のゲインと位相
以上より、レギュレータ全体のゲインと位相は次のように計算できます。
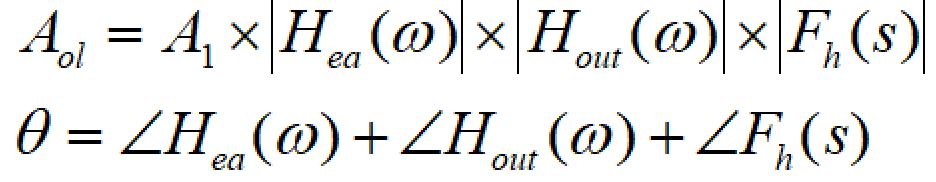
絶対値の計算方法、偏角の計算方法は下記記事をご覧ください。
上記計算式を用いてエクセルでボーデ線図を描かせると下図のようになります。
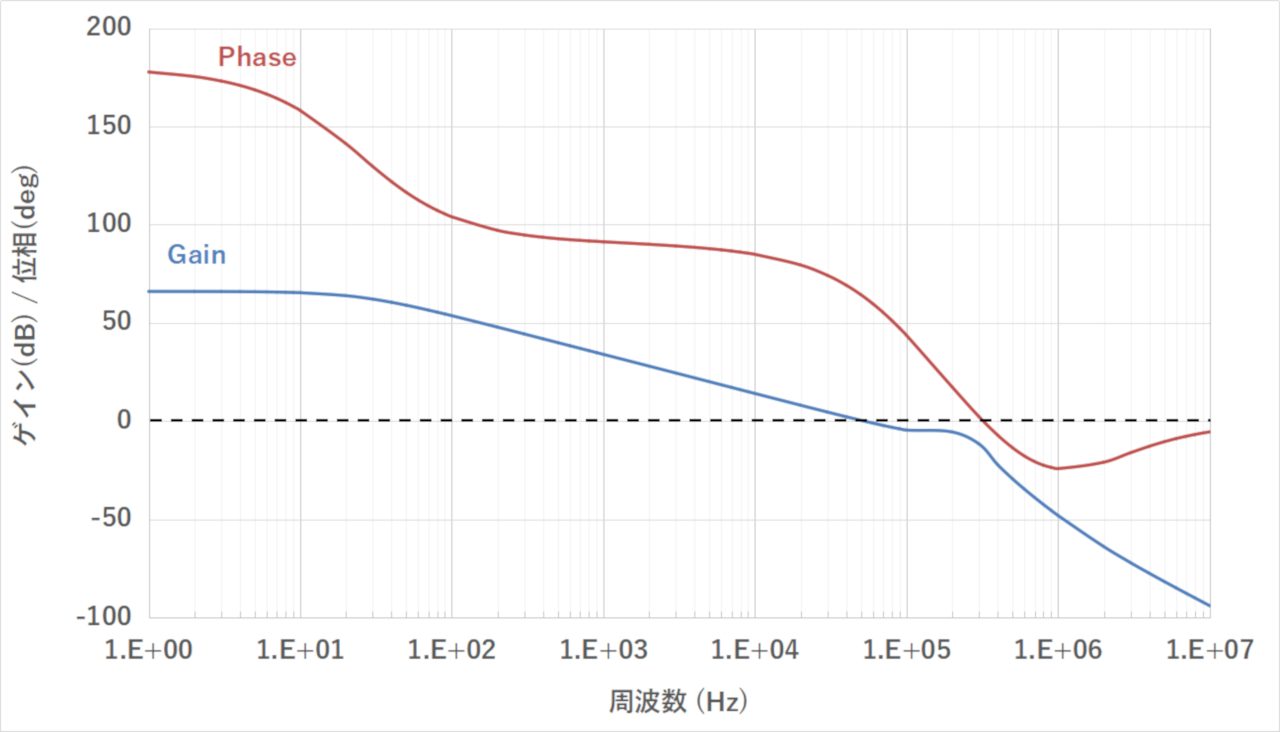
エクセルで作成した計算シートは以下よりダウンロードして頂けます。
電圧モードの位相補償と計算
下図のような降圧型の電圧モードスイッチングレギュレータを考えます。
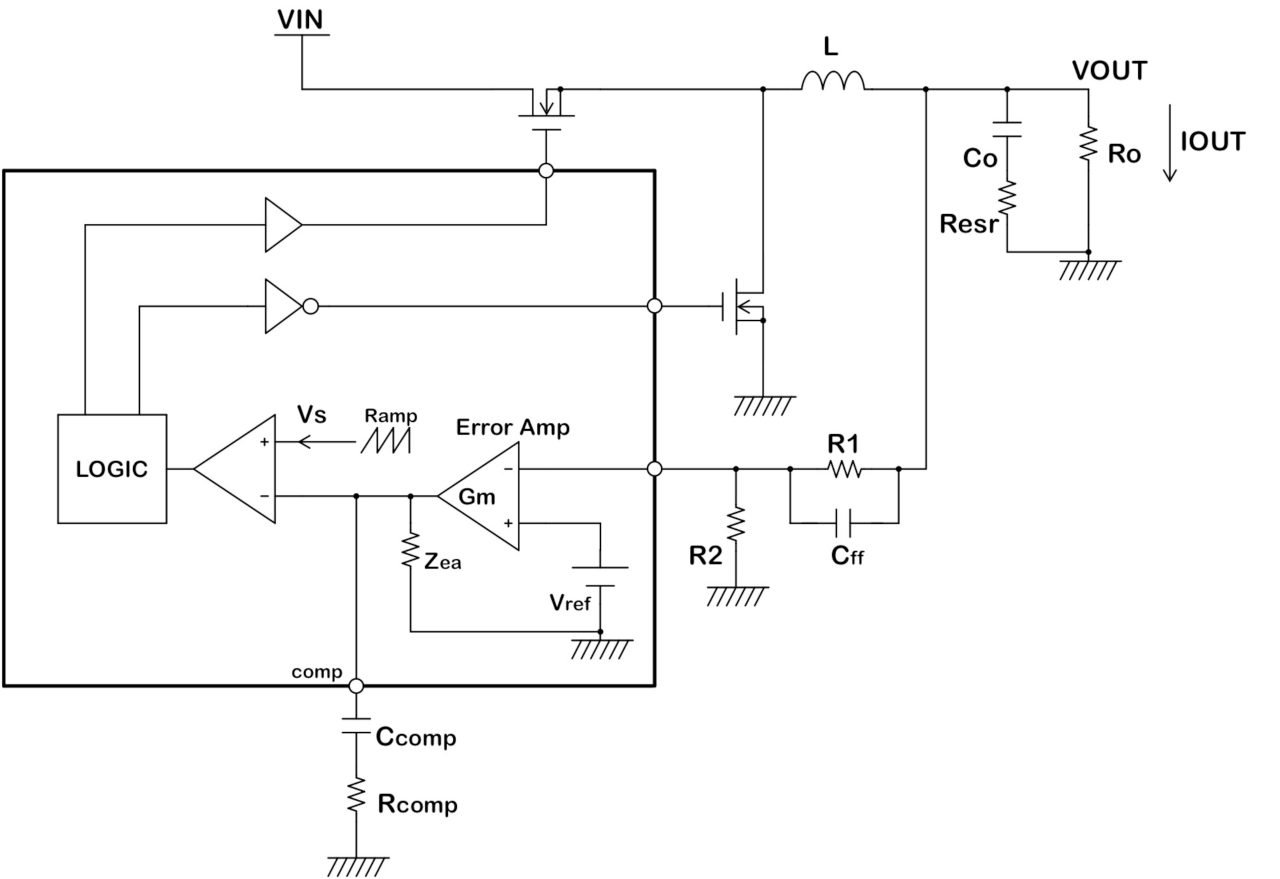
オープンループゲイン
電流モードと同様、まずはオープンループゲインから計算していきます。
フィードバック部、エラーアンプ部のゲインは電流モードと同様で下記のようになります。
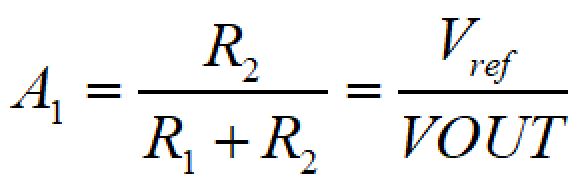
![]()
次にエラーアンプの出力部からスイッチノード(上下のFETの中点)までの増幅率を計算します。
エラーアンプ出力と比較するランプ波形(三角波、またはノコギリ波)の振幅をΔVsとすると、増幅率は
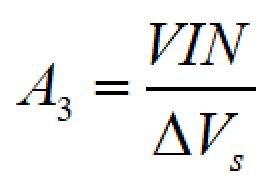
となります。
これらの積を取ることでオープンループゲインを計算することができます。
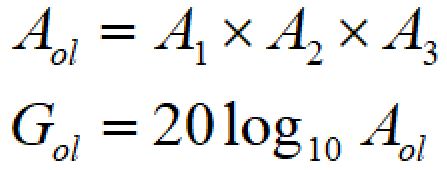
簡単な位相補償の手順
電圧モードの位相補償の手順は、
- SW周波数の1/10で0dBになるように1stポールを設定
- LCフィルタの共振周波数にエラーアンプ部で作ったゼロを当てる
- LCフィルタの共振周波数にフィードバック部で作ったゼロを当てる
となります。
LCフィルタによって生じるダブルポールを2つのゼロでキャンセルさせるという方法です。
理由は後述しますが、電圧モードの場合、簡易計算では電流モードほど上手くいかないことがほとんどです。
ですが、当たりを付けるための指標としては有用ですので活用してみてください。
1stポールの設定
電流モードと同様、下記のように計算できます。
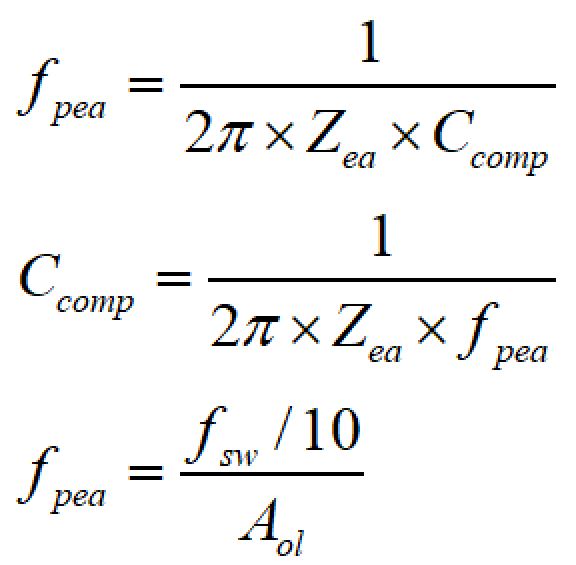
エラーアンプ部のゼロの設定
出力部のLCフィルタによる共振周波数は以下の式で与えられます。
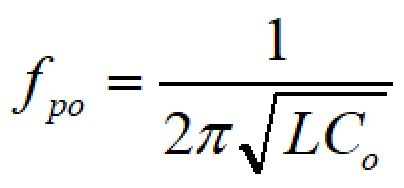
エラーアンプ部のゼロは下記のように計算されます。
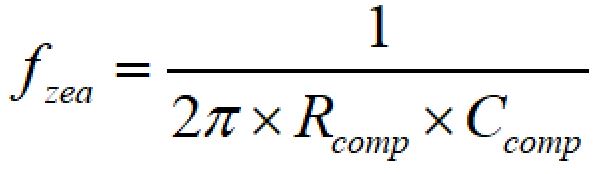
fpo = fzeaとするためのRcompは、
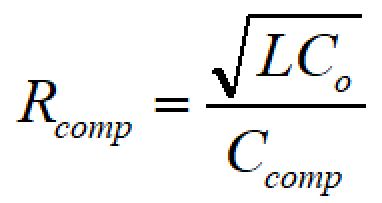
となります。
フィードバック部のゼロの設定
フィードバック抵抗:R1と並列にコンデンサを挿入することでゼロを生成できます。
ゼロの周波数は、
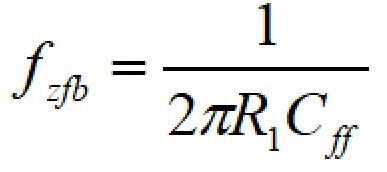
fpo = fzfbとするためのCffは、
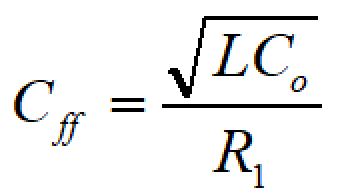
となります。
以上が簡易的な位相補償の手順になりますが、位相余裕が思ったほど稼げない場合がほとんどだと思います。
伝達関数を計算することで、その理由を理解し、位相補償の最適化を行うことができます。
伝達関数を計算して位相余裕度を計算する
VOUTを起点に一周するループを考えます。
フィードバック部
前述の通り、電圧モードの場合フィードバック部にフィードフォワードコンデンサ:Cffを追加してゼロを作ります。
したがって、伝達関数は、
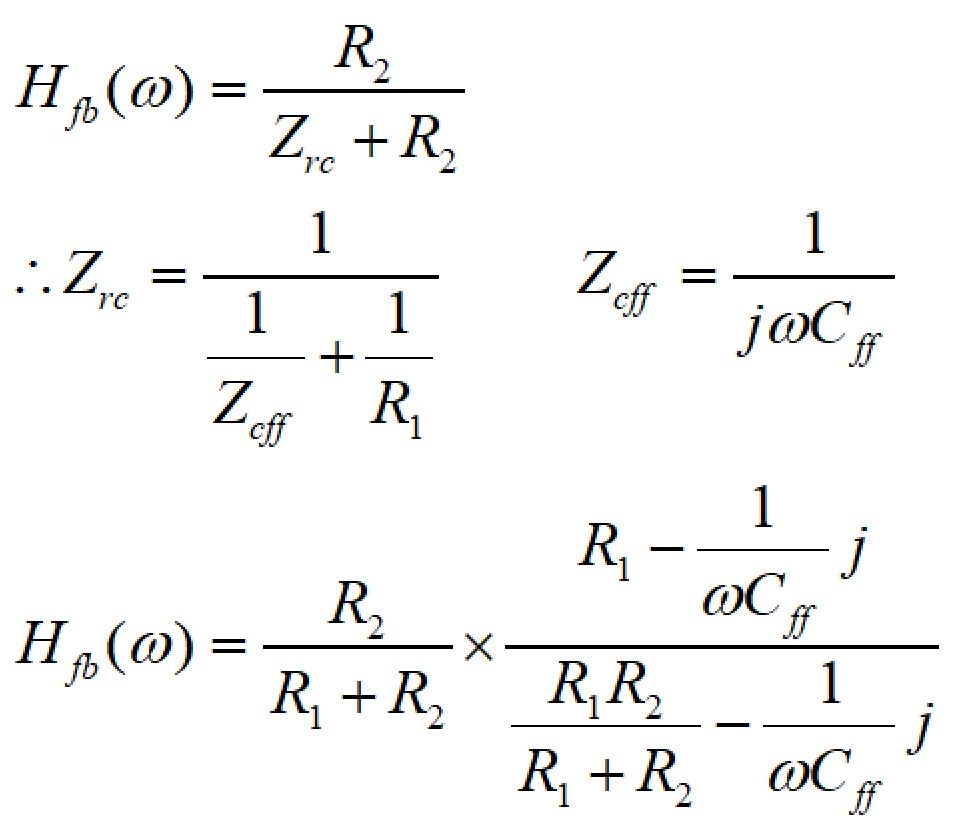
となります。
エラーアンプ部
エラーアンプの入力から出力までの伝達関数を考えます。
電流モードと同様、以下のように計算できます。
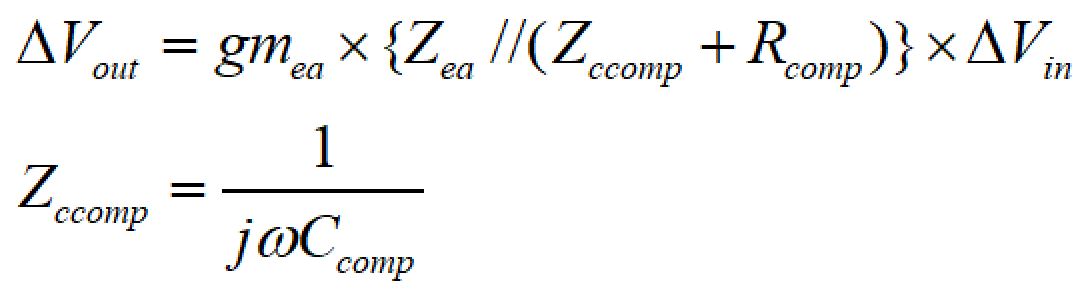
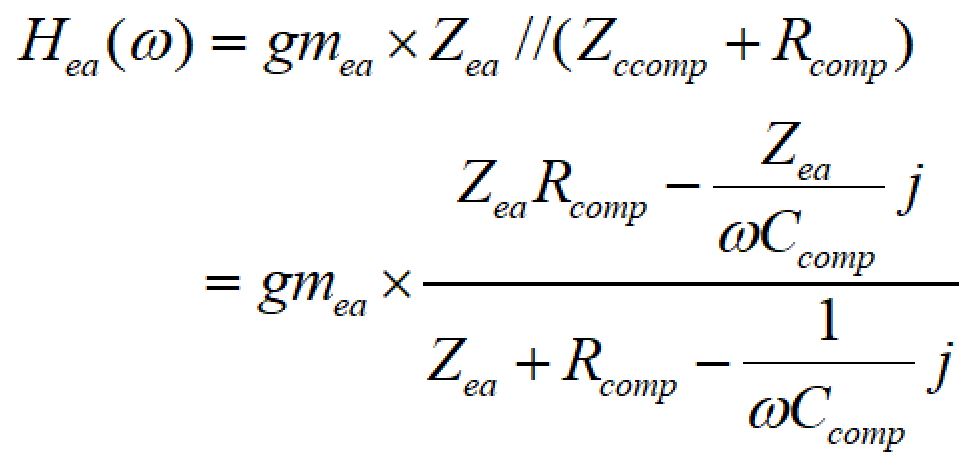
エラーアンプ出力からスイッチノードまで
この部分は位相遅れも位相進みもありませんので、増幅率だけ考えます。
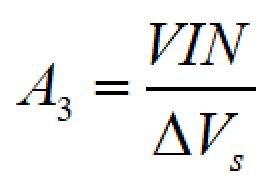
LCフィルタ部
スイッチノードを入力として出力電圧を計算します。
LCを周波数特性を持った抵抗と考え、抵抗分割の要領で計算できます。
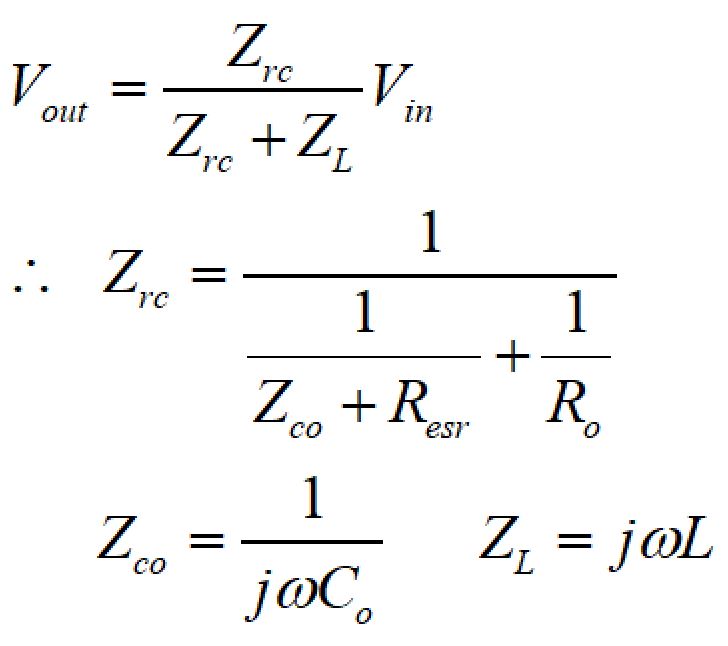
したがって、伝達関数は、
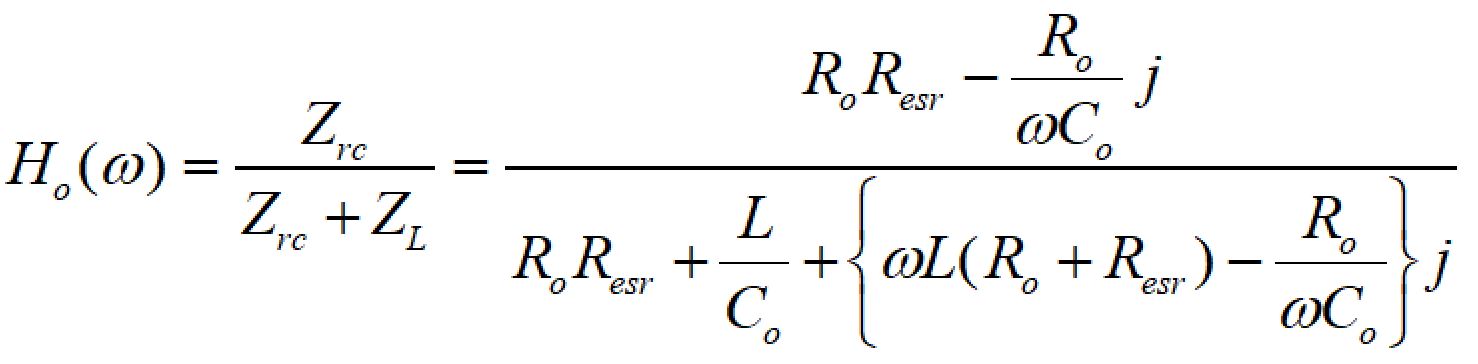
となります。
レギュレータ全体のゲインと位相
以上より、レギュレータ全体のゲインと位相は次のように計算できます。
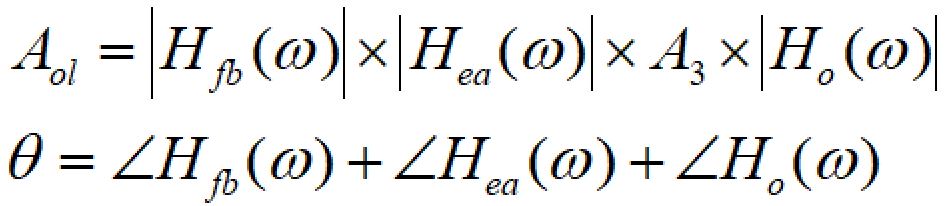
上記計算式を用いてエクセルでボーデ線図を描かせると下図のようになります。
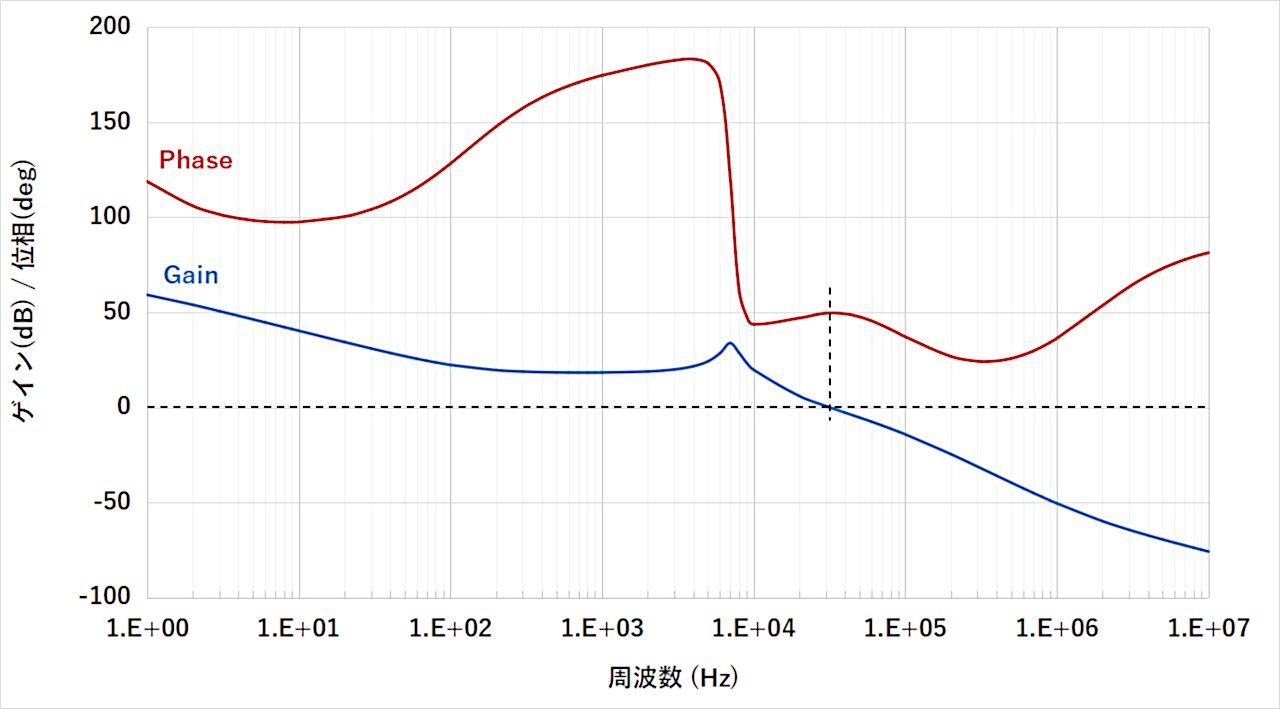
エクセルで作成した計算シートは以下よりダウンロードして頂けます。
電圧モードの位相補償が難しい理由
電圧モードはLCフィルタによるダブルポールができるため位相補償が難しいと良く言われますが、真因ではありません。
問題はフィードバック抵抗部分に設置するゼロにあります。
前記のフィードバック部分の伝達関数を使って、周波数特性をグラフ化すると下図のようになります。
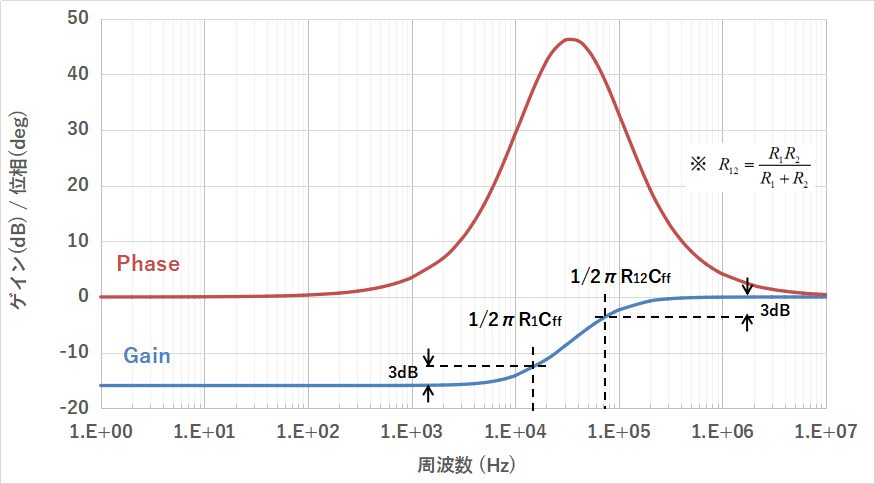
上図を見て分かる通り、R1とCffで進んだ位相が、R1とR2の合成抵抗とCffによって元に戻ります。
これにより、期待したほどゼロによる効果が得られず、位相余裕が確保できないのです。
R1とR2の値が近いほどゼロによる効果が減少していきますので、出力電圧が低くなるほど(出力電圧とVrefの電圧が近くなるほど)Cffによる効果が無くなっていき、位相余裕度が悪化します。
電圧モードは電流モードに比べ位相補償が難しいと言われる理由はここにあります。
対策としては、出力コンデンサのESRを積極的に位相補償に使うという方法があります。
この場合は単純な位相進みになるので位相補償が簡単になります。
ただし、電解コンデンサなどを使う場合は狙った周波数にゼロを持ってくることは難しいので、セラミックコンデンサと直列に抵抗を入れるという方法が考えられます。
デメリットとしては、出力に発生するリップル電圧が大きくなってしまうということです。
こういった課題が無い分、電流モードの方が使いやすいと言えます。
