インバーテッドダーリントン接続の特徴と発振対策
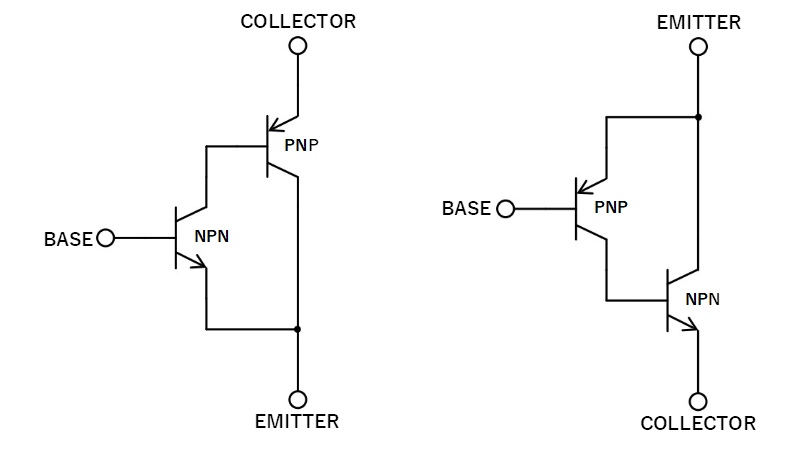
インバーテッドダーリントン接続とは、NPNトランジスタとPNPトランジスタ組み合わせて構成した高hFEの増幅回路です。
NPN-PNP接続はNPNトランジスタと等価、PNP-NPN接続のものはPNPトランジスタと等価となります。
PNP-NPN接続のものは疑似PNPと呼ばれることもあります。
インバーテッドダーリントンの動作原理
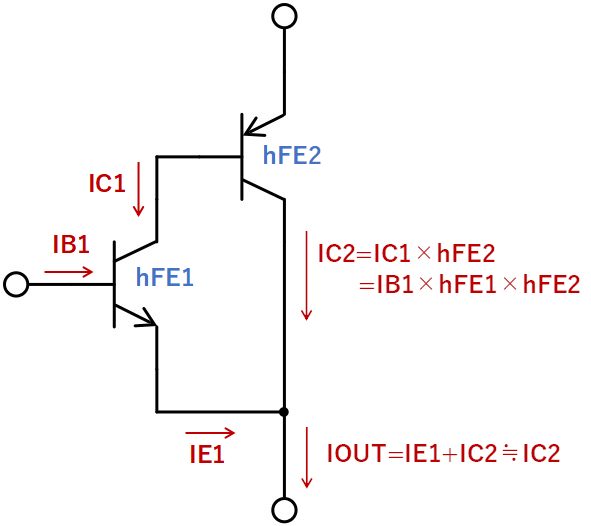
NPNトランジスタに入力されたベース電流:IB1が増幅され、IC1=hFE1×IB1の電流がPNPトランジスタのベースから引き込まれます。
この電流がPNPトランジスタでさらに増幅され、
IC2 = IC1 × hFE2 = IB1 × hFE1 × hFE2
の電流がコレクタ側に出力されます。
出力電流はIC2とIE1の合計値ですが、IC2>>IE1なので、出力電流:IOUTは
IOUT ≒ IC2 = IB1 × hFE1 × hFE2
となり、hFE1 × hFE2倍の電流増幅率となることが分かります。
インバーテッドダーリントンのメリットとデメリット
通常のダーリントン接続は、入力電圧が2VBE以上ないと動作できませんでしたが、インバーテッドダーリントンの場合はVBEだけで動作が可能です。
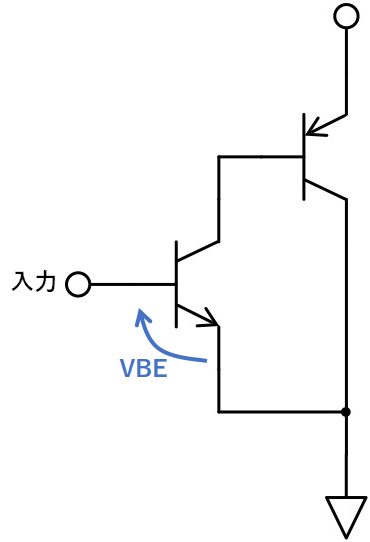
欠点としては発振しやすいことが挙げられます。
インバーテッドダーリントン接続は、負帰還を形成しています。
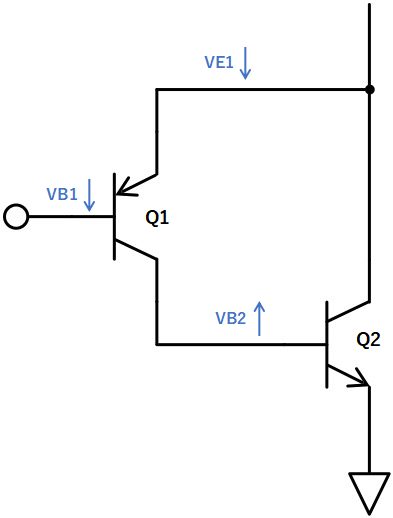
下図のように入力電圧:VB1が低下すると、Q1のVBEが開くためコレクタ電流が増加し、VB2が上昇します。
VB2が上昇するとQ2のVBEが開くためQ2のコレクタ電流が増加し、Q2のコレクタ電圧=Q1のエミッタ電圧:VE1が下がります。
VE1が下がるとQ1のVBEが低下し、VB2は低下するという動きになります。
低周波領域ではこのように負帰還となっているため発振しませんが、高周波領域ではNPNトランジスタのベース-コレクタ間寄生容量によって、正帰還(フィードフォワード)が形成されます。
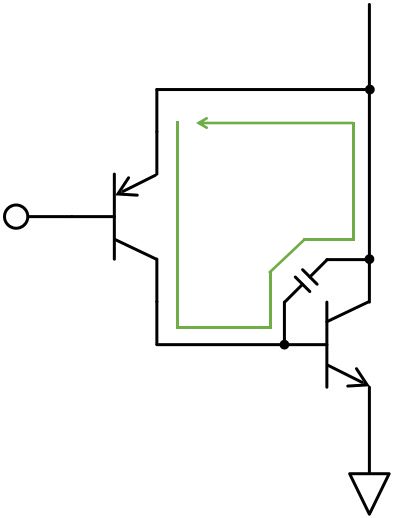
このループはRHPゼロを形成します。
インバーテッドダーリントン単体で発振することはあまりありませんが、オペアンプやレギュレータ内の増幅段としてインバーテッドダーリントンが使われていると、このRHPゼロの影響で発振することがあります。
インバーテッドダーリントンの発振対策
寄生容量:Cpによってできる正帰還を、PNPトランジスタのベース-コレクタ間容量:C1を追加することで、全体として負帰還に戻し、発振を抑えることができます。
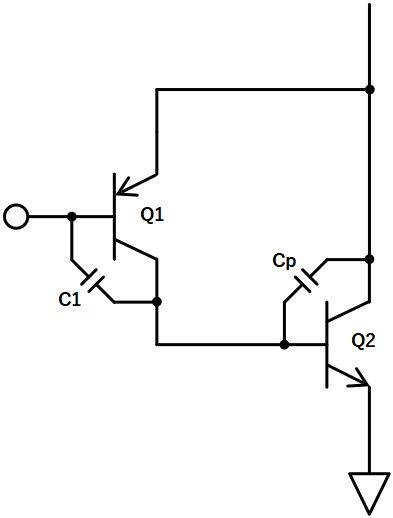
C1とCpで2つのフィードフォワードができることで、打ち消すことができるのです。
