RCフィルタとLCフィルタの伝達関数を計算する方法

アナログ回路設計者にとって、伝達関数は取っ付きにくく苦手意識がある方も少なくないでしょう。
ここでは、よく使うRCフィルタ、LCフィルタに絞って伝達関数を分かりやすく解説していきたいと思います。

LCのインピーダンス

はじめにLCのインピーダンスの計算式を確認します。
インピーダンスは、周波数依存性を含んだ抵抗値と考えると分かりやすいと思います。

フィルタの設計経験があれば感覚的には理解していると思いますが、コンデンサは高周波側でインピーダンスが下がっていきます。
逆にコイルは高周波側でインピーダンスが上昇していきます。

式で表すと次のようになります。

コンデンサのインピーダンス

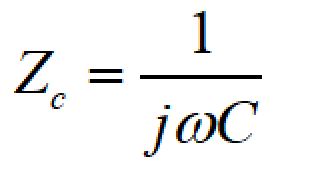
コイルのインピーダンス

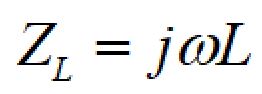
ωは角周波数で、周波数:fとの関係は下記のようになります。

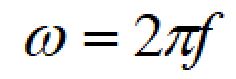
RCフィルタの伝達関数

伝達関数とは、入力と出力の関係を表す数式です。
これだけだとイメージしにくいので、RCフィルタの例で具体的に考えてみます。

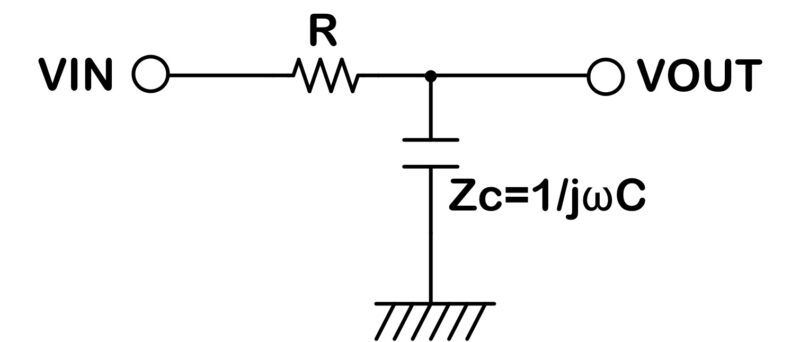
コンデンサを周波数特性のある抵抗成分と考えれば、VOUTはVINをRとCで抵抗分割した値になると考えることができます。
したがって、VINとVOUTの関係式は以下のように表すことができます。

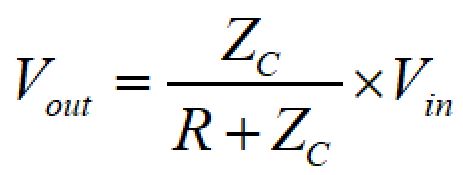
このVINに掛かる係数部分が伝達関数となります。
よって、RCフィルタの伝達関数は、

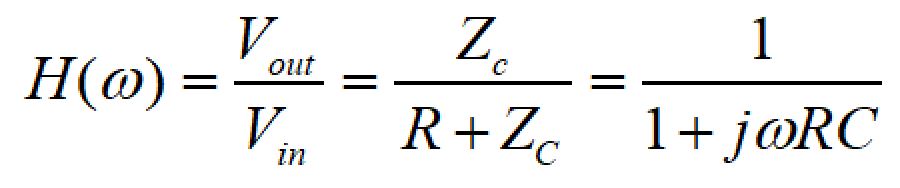
となります。

伝達関数はベクトルですので複素数を含んでいます。
絶対値を取ることで大きさを求めることができます。

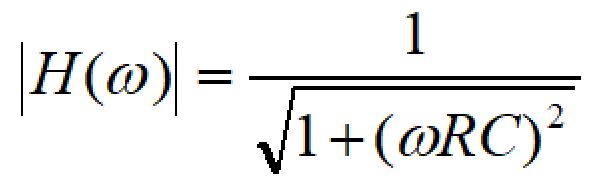
伝達関数は入力と出力の比、つまりゲインを表しています。
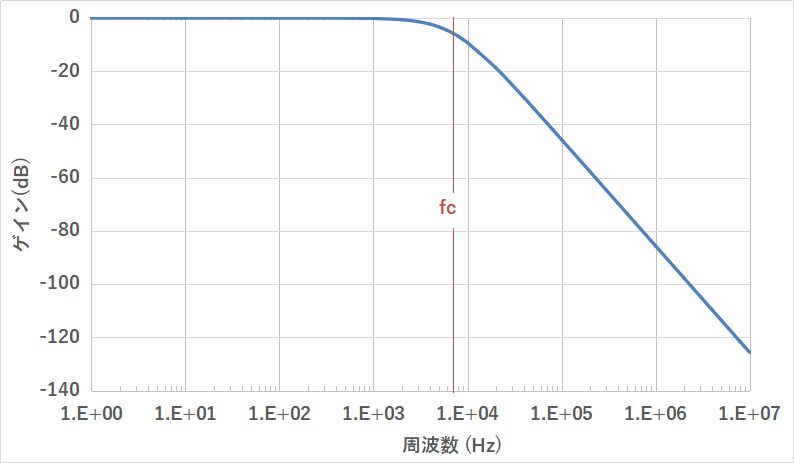
伝達関数の絶対値をdB表示にすることで、20dB/decadeで減衰するRCフィルタの代表的な周波数特性を得ることができます。

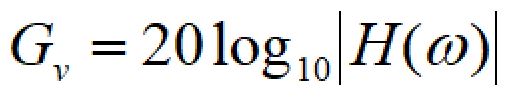
横軸に周波数を取って、エクセルで上記計算式でグラフを描かせると、以下のような周波数特性図が得られます。

カットオフ周波数は以下の計算式で求めることができます。

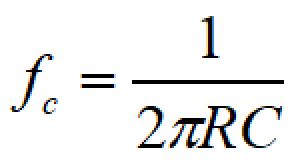
周波数特性を計算したエクセルシートは以下よりダウンロードできます。

LCフィルタの伝達関数

下記のようなLCフィルタ回路を考えます。
負荷Rがあるため、LCRの伝達関数を考えることになります。

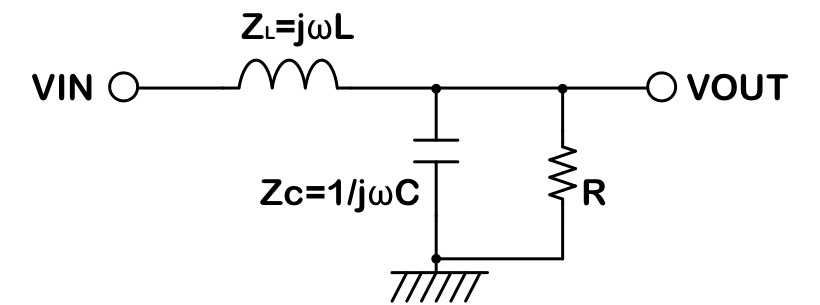
RCフィルタと同様に考えると、VOUTはVINはLと、RCの合成インピーダンスとの分割になります。
したがって、伝達関数、ゲインは次のように求めることができます。

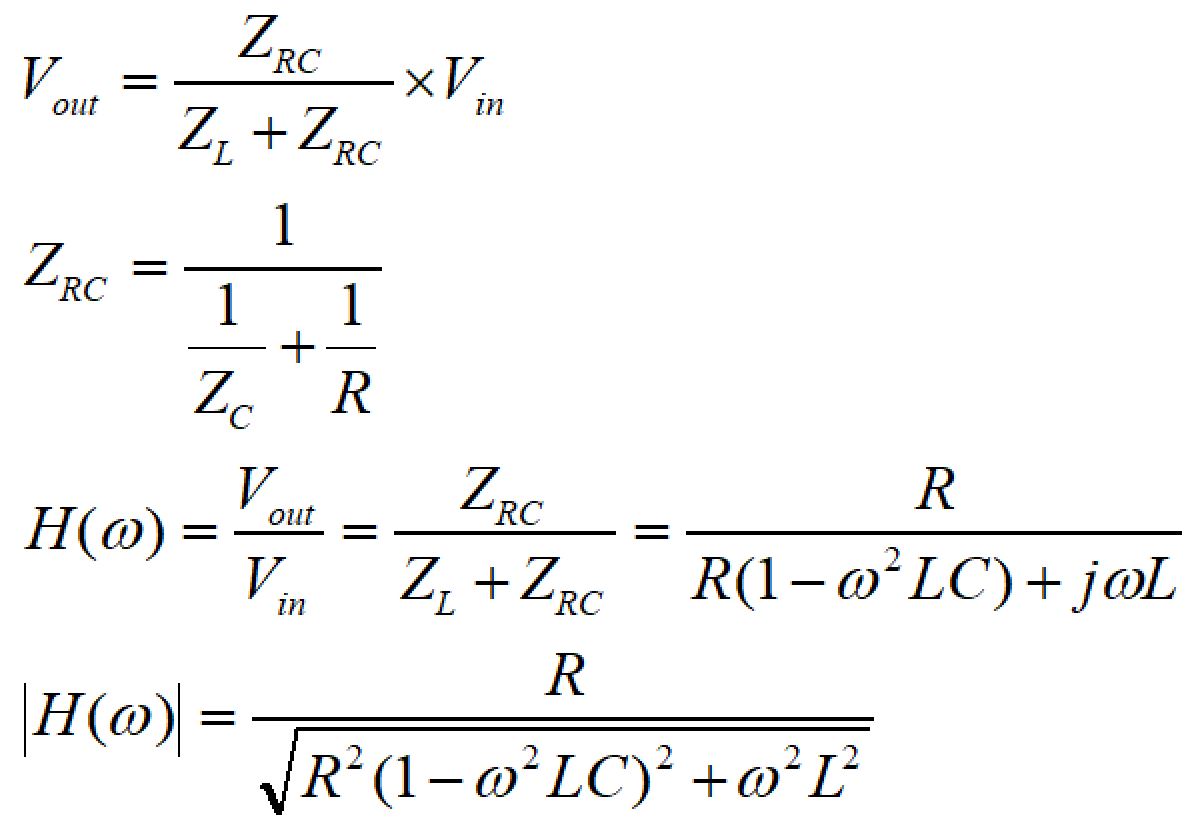
エクセルで周波数特性を描かせると以下のようになります。

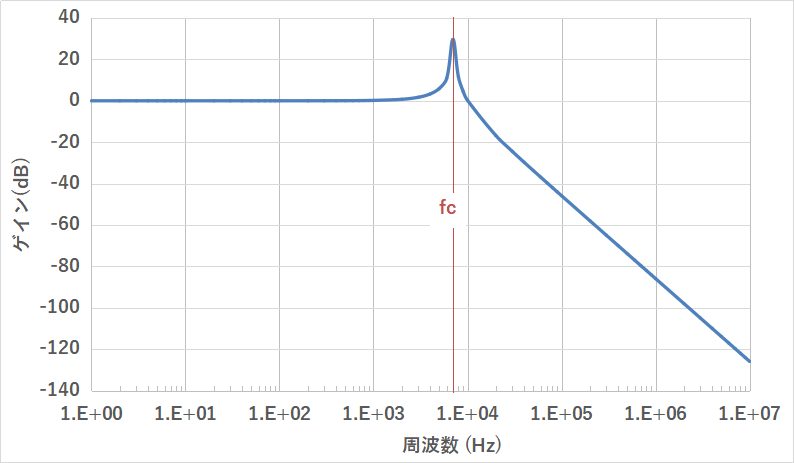
カットオフ周波数は以下の計算式で求めることができます。

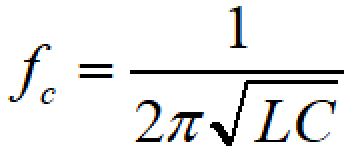
周波数特性を計算したエクセルシートは以下よりダウンロードできます。