LCフィルタの設計方法
LCフィルタとは、コイルとコンデンサを組み合わせて任意の周波数帯域の信号を遮断したり通過させたりする回路です。
LとCの2つのリアクタンスを持った2次フィルタなので、1次フィルタであるRCフィルタよりシャープな特性が得られます。
本稿では、LCフィルタの設計計算、部品定数の選定方法について解説していきます。
LCフィルタの用途
LCフィルタの用途は
- ローパスフィルタ
- ハイパスフィルタ
- バンドパスフィルタ
の3つがあります。
ローパスフィルタ
ローパスフィルタは低周波と通過させ高周波を遮断します。
高周波ノイズの除去やオーディオの高音域のカットなどに使われます。
ローパスフィルタには4つの種類があります。
L型フィルタ(L-C型)
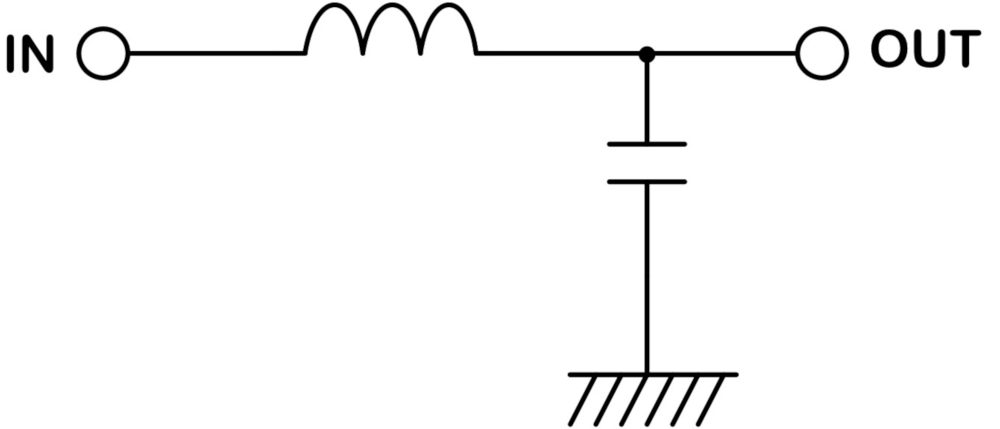
最も良く使われるLCフィルタの形です。
インダクタは高周波を高インピーダンスで遮断し、コンデンサは高周波を低インピーダンスでバイパスします。
したがって、この回路では入力側のインピーダンスが低く、出力側のインピーダンスが高い場合に使われます。
L型フィルタ(C-L型)
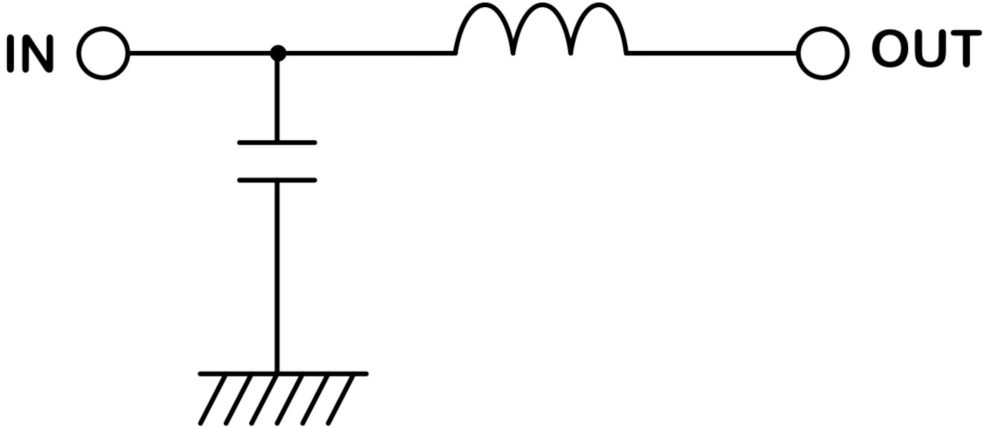
L-C型とは逆で、入力側のインピーダンスが高く、出力側のインピーダンスが低い場合に使われます。
π型フィルタ
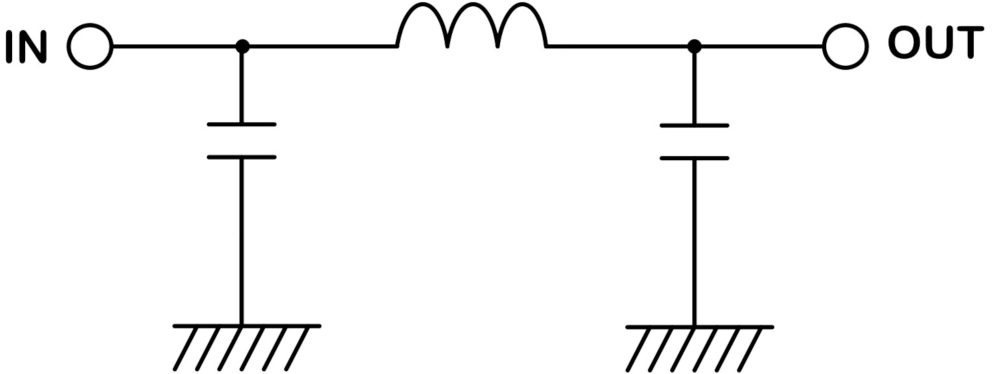
ギリシャ文字のπ(パイ)の形になっていることからπ型フィルタと呼ばれます。
入出力側ともにコンデンサが接続されているため、入力側のインピーダンス、出力側のインピーダンスともに高い場合に使われます。
T型フィルタ
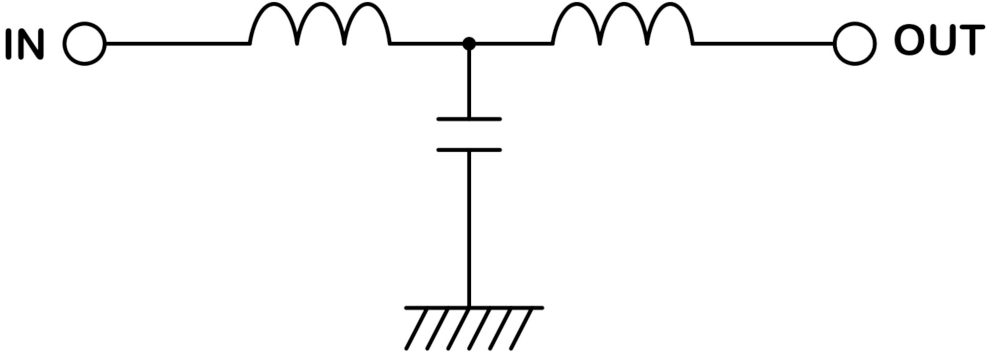
アルファベットのTの形になっていることからT型フィルタと呼ばれます。
入出力側ともにインダクタが接続されているため、入力側のインピーダンス、出力側のインピーダンスともに低い場合に使われます。
ハイパスフィルタ
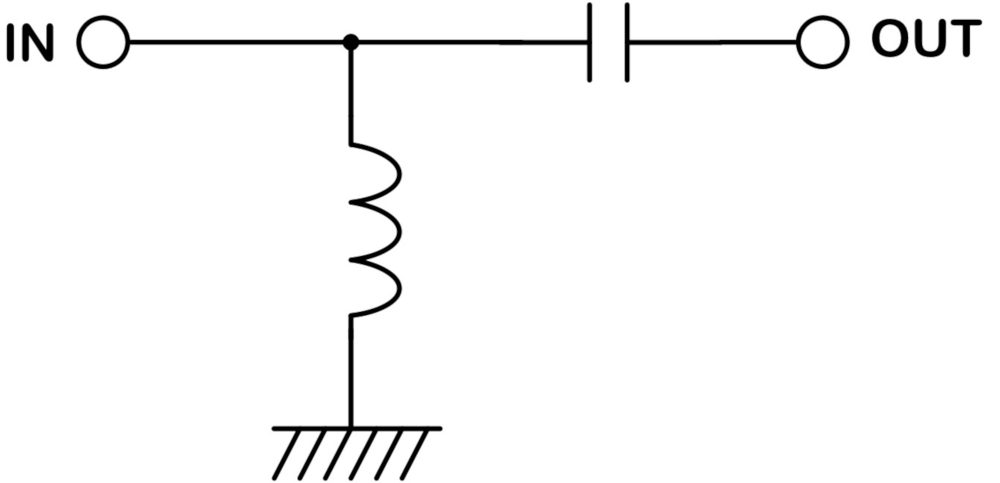
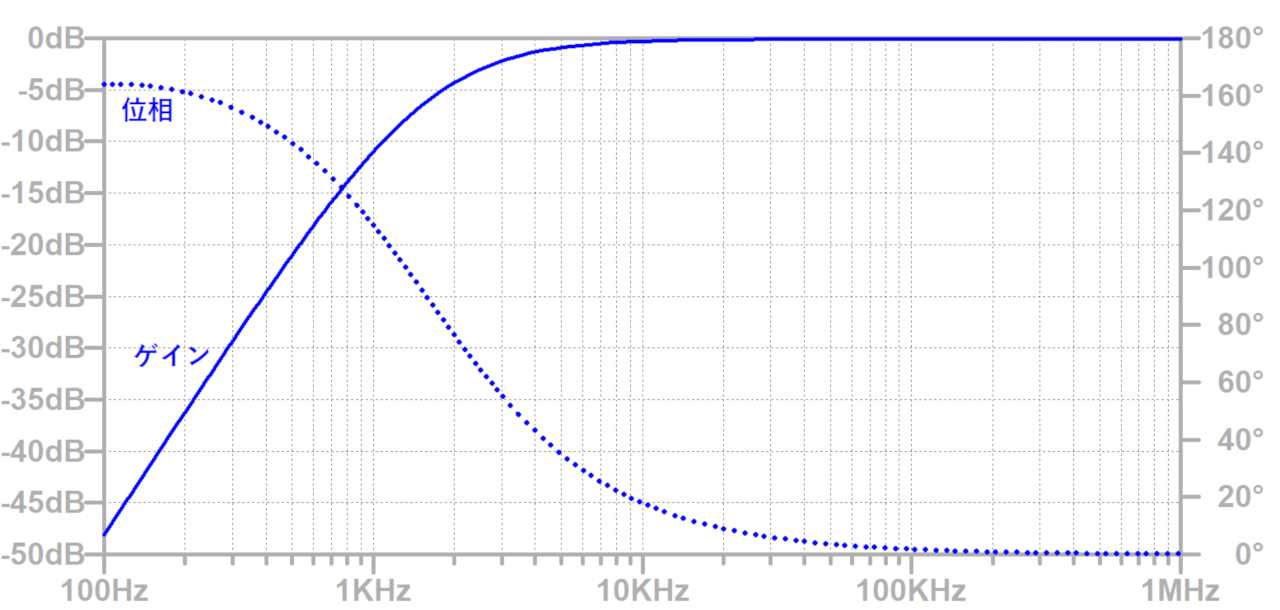
ハイパスフィルタは低周波を遮断し、高周波を通過させます。
オーディオの低音域のカットなどに使われます。
バンドパスフィルタ
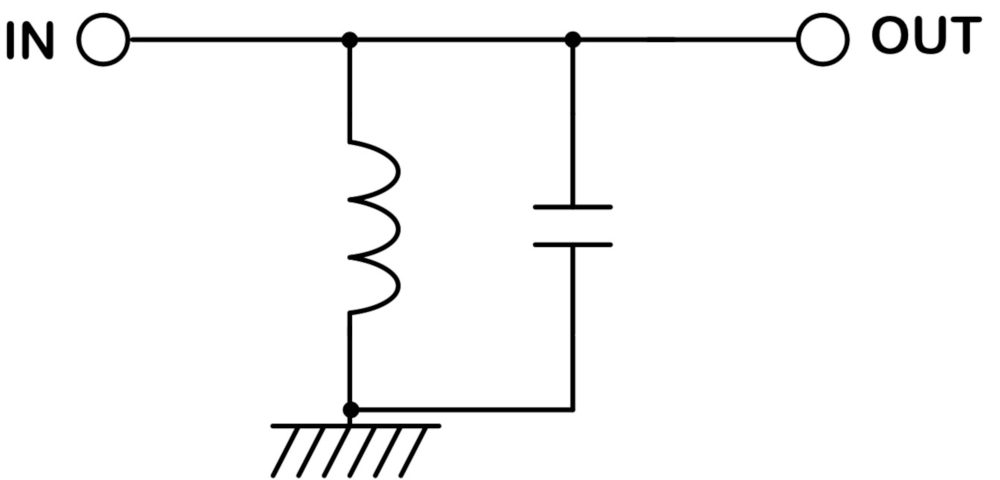
バンドパスフィルタは特定の周波数帯域のみ通過させます。
選局したラジオの受信周波数に合わせて帯域を設定するなどの用途で使われます。
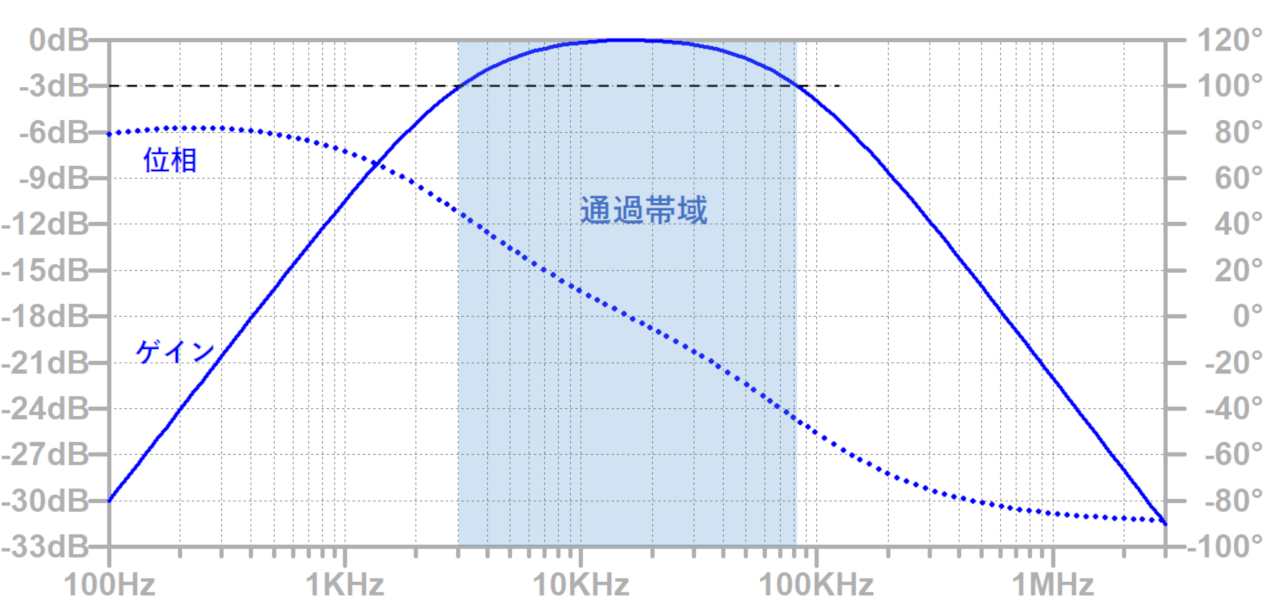
LCフィルタの設計
LCローパスフィルタを考えます。

カットオフ周波数の計算
カットオフ周波数は以下の式で計算できます。
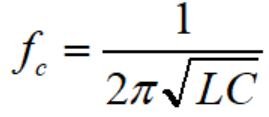
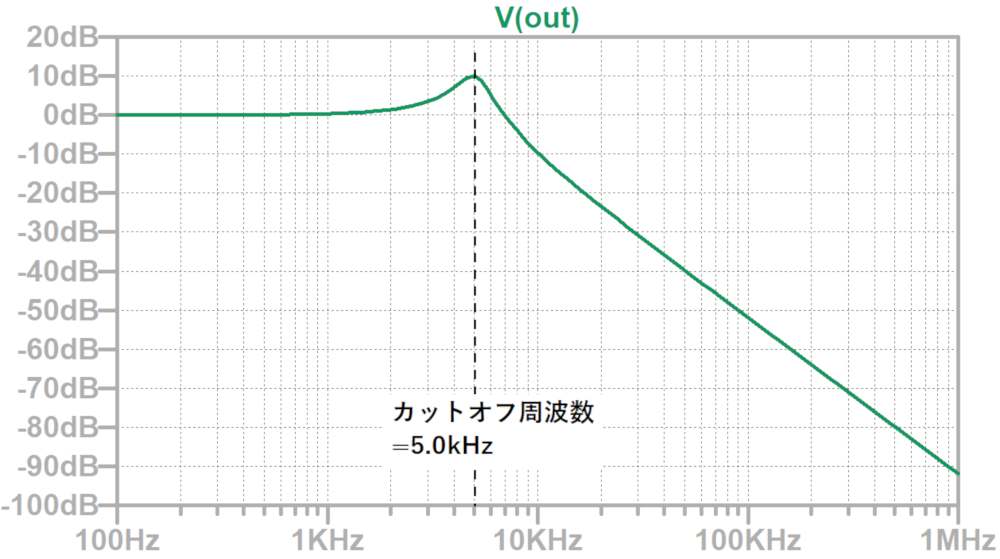
L=10uH、C=100uFとすると、カットフ周波数は5.0kHzとなります。
伝達関数
LCフィルタの伝達関数は以下のようになります。
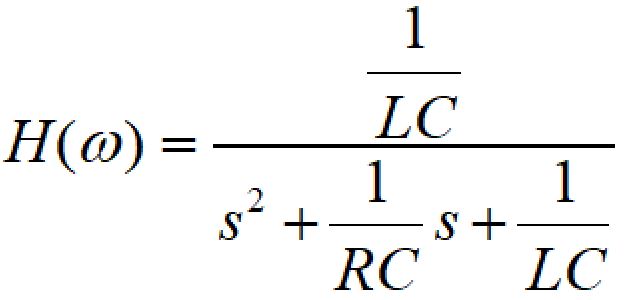
Rは出力側の負荷抵抗です。
Q値の計算
Q値はQuality factorの頭文字を取っており、フィルタのQuality(質)を定量的に表す値です。
Q値が高いほどフィルタの特性が鋭くなります。
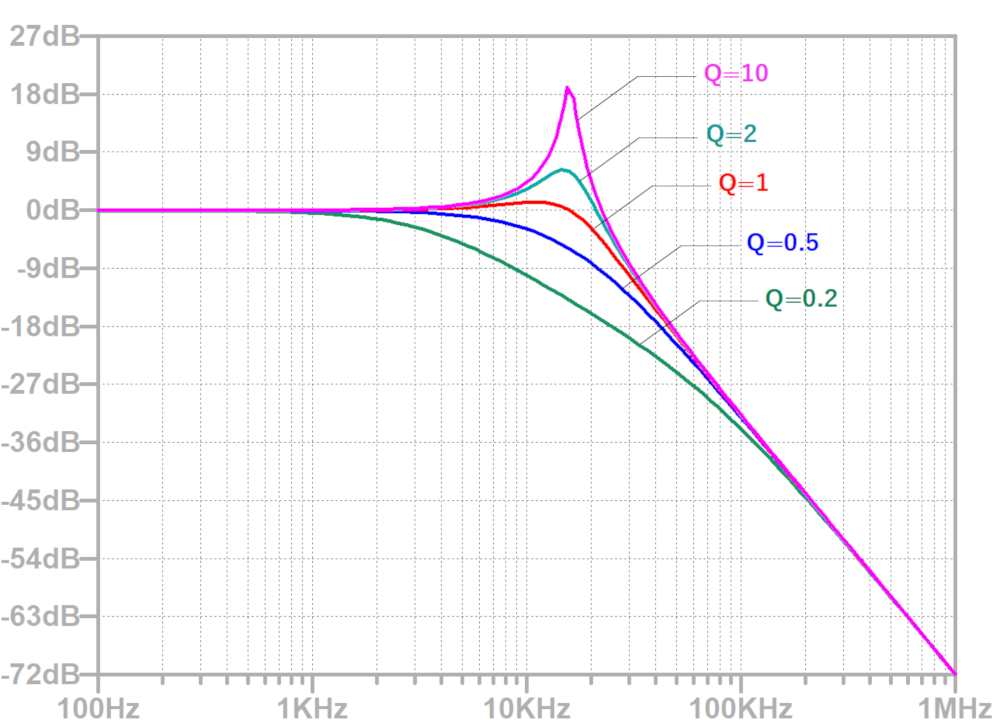
Q値は以下の式で計算できます。
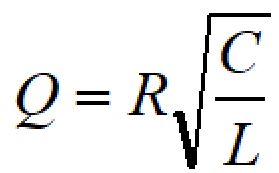
設計ツールを使って設計する
これまでは理想的な条件での計算方法について解説してきました。
しかし、ノイズ対策などでより高周波の特性が必要になる場合、素子の寄生パラメータも含めて考える必要があります。
そのため、机上で計算するには複雑になるのでツールを使って設計を進めます。
ここでは、LTspiceを使って特性をシミュレーションする方法について解説していきます。
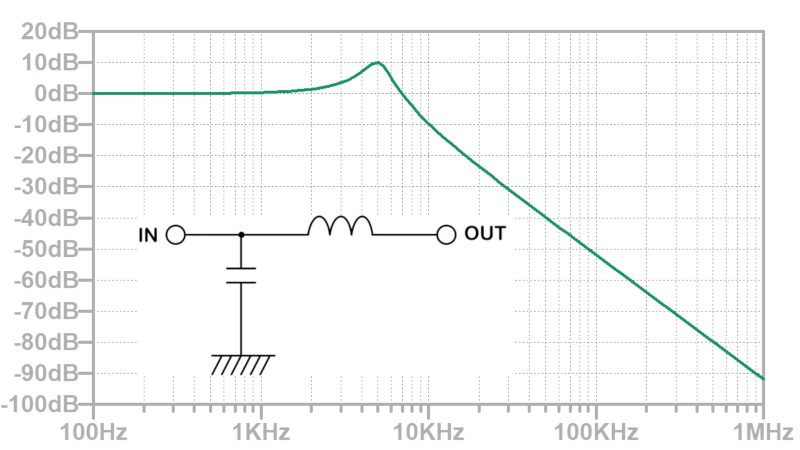
LCの寄生素子を含めて、下図のようなπ型フィルタを考えます。
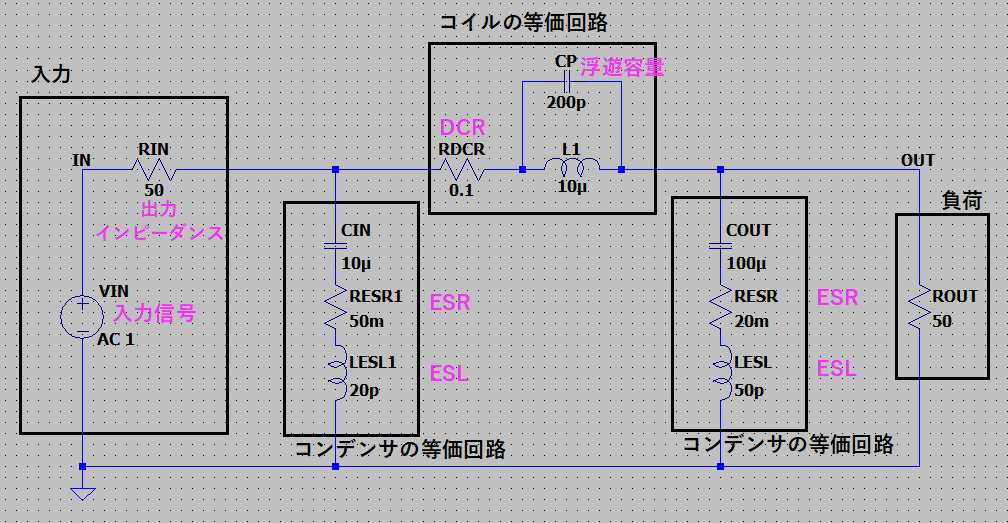
この回路でAC解析を行うと以下のような周波数特性になります。
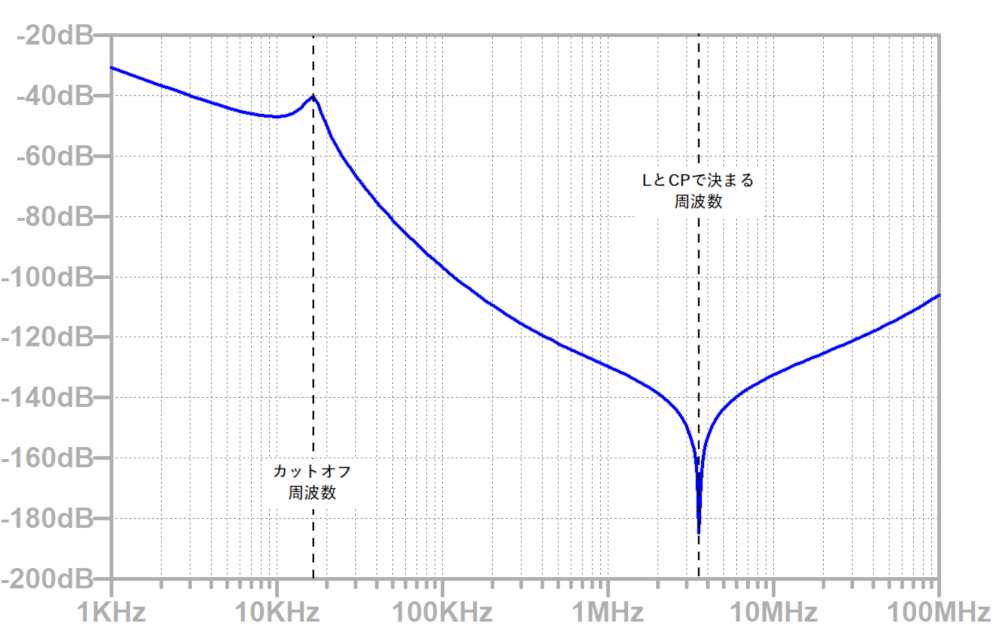
3.6MHz付近でコイルの浮遊容量によりインピーダンスが下がり、ノイズ除去性能が悪化します。
コンデンサもESR、ESLの影響で高周波でインピーダンスが大きくなるため、やはりノイズ除去性能が悪化します。
このように、高周波のノイズ除去の特性を確認するためには、寄生素子の影響も考慮に入れる必要があります。
LCフィルタとRCフィルタの違い
同じカットオフ周波数のRCローパスフィルタとLCローパスフィルタの特性を比較します。
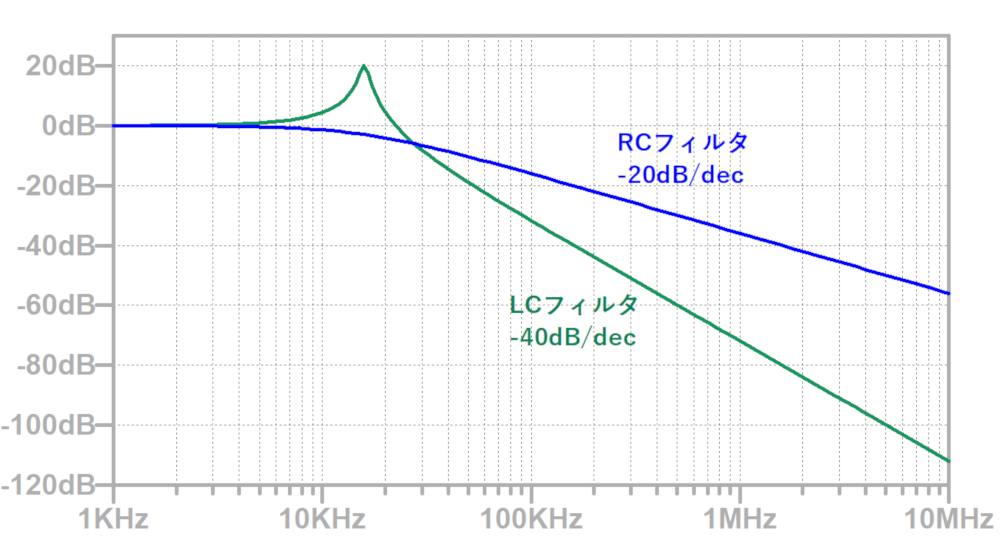
RCフィルタの減衰特性は-20dB/decですが、LCフィルタは-40dB/decとなり、LCフィルタの方がシャープな特性を得られます。
LとCはインピーダンスにリアクタンス(虚数成分)を持つため、LCフィルタは2次フィルタ、RCフィルタは1次フィルタと呼ばれ、これが特性の差に現れます。
下記の記事でRLCのインピーダンス、リアクタンスについて解説しています。
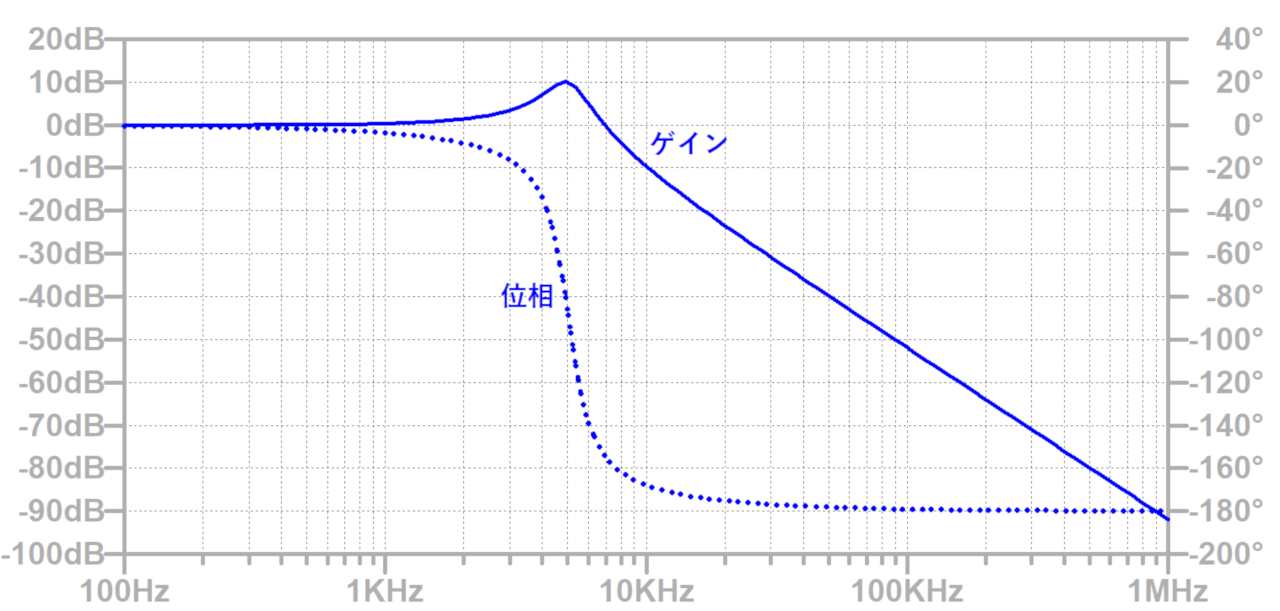
また、LCフィルタの場合は共振周波数でゲインの盛り上がりができます。
入力にステップ変動を与えると、LCフィルタの場合は共振周波数でリンギングが発生します。
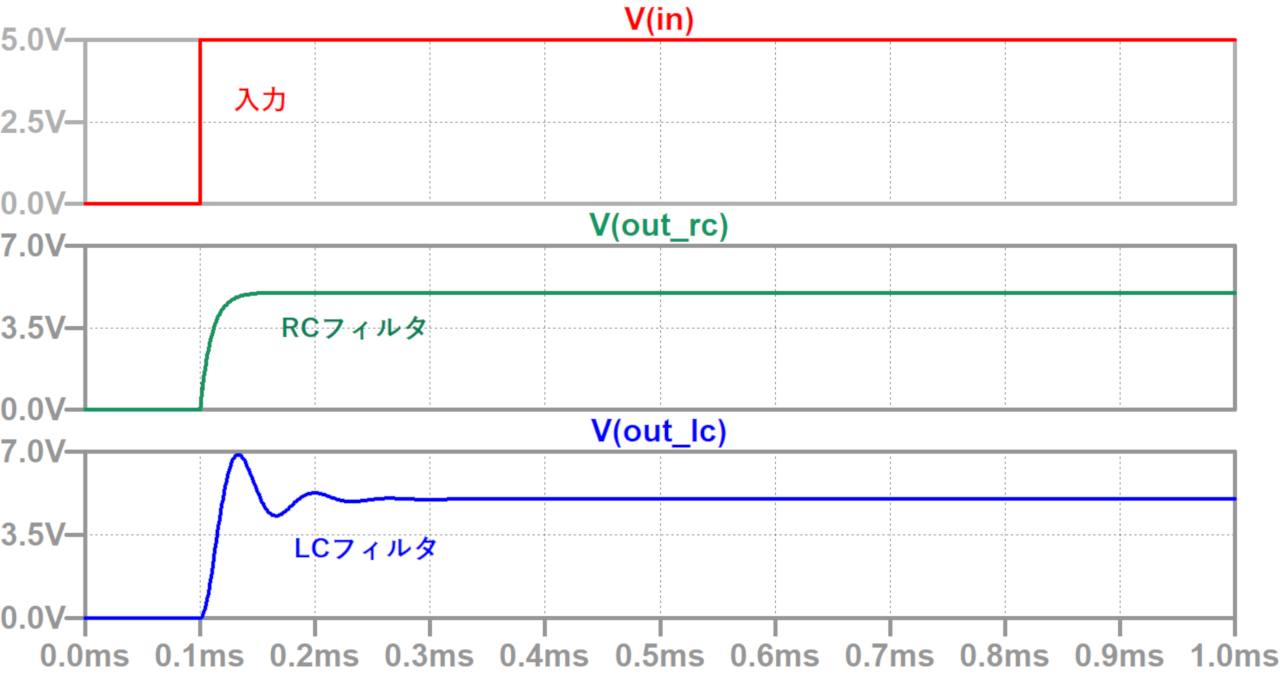
Q値が大きいほどリンギングの振幅が大きくなります。
Analogistaでは、電子回路の基礎から学習できるセミナー動画を作成しました。
電子の動きをアニメーションを使って解説したり、シミュレーションを使って回路動作を説明し、直感的に理解しやすい内容としています。
これから電子回路を学ぶ必要がある社会人の方、趣味で電子工作を始めたい方におすすめの講座になっています。