インピーダンスとは?わかりやすく解説

インピーダンスとは、交流回路における電流の流れにくさを数値化したもので、電圧と電流の比を表します。
単位はΩで、直流回路の抵抗の考え方を複素数にまで広げたものです。
複素数の概念が出てくることで分かりにくくなってしまいますが、ここではインピーダンスとは何なのか、抵抗との違いは何なのかということをわかりやすく解説していきたいと思います。
インピーダンスとは何か
インピーダンスは電圧と電流の比です。
したがって、インピーダンス:Zは以下の式で表されます。
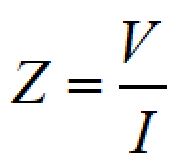
単位はΩなので、直流回路の R = V / I と同じ形です。
つまり、交流回路では抵抗をインピーダンスに置き換えてオームの法則を使うことができます。
この式を書き換えると、
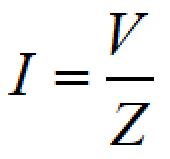
となり、インピーダンスが大きいほど電流が小さくなるため、インピーダンスは電流の流れにくさを表していることが分かります。
抵抗とインピーダンスとリアクタンスの違い
インピーダンスは周波数によって値が変化しないレジスタンス(抵抗)と周波数によって電流の流れにくさが変わるリアクタンスを合わせたものです。
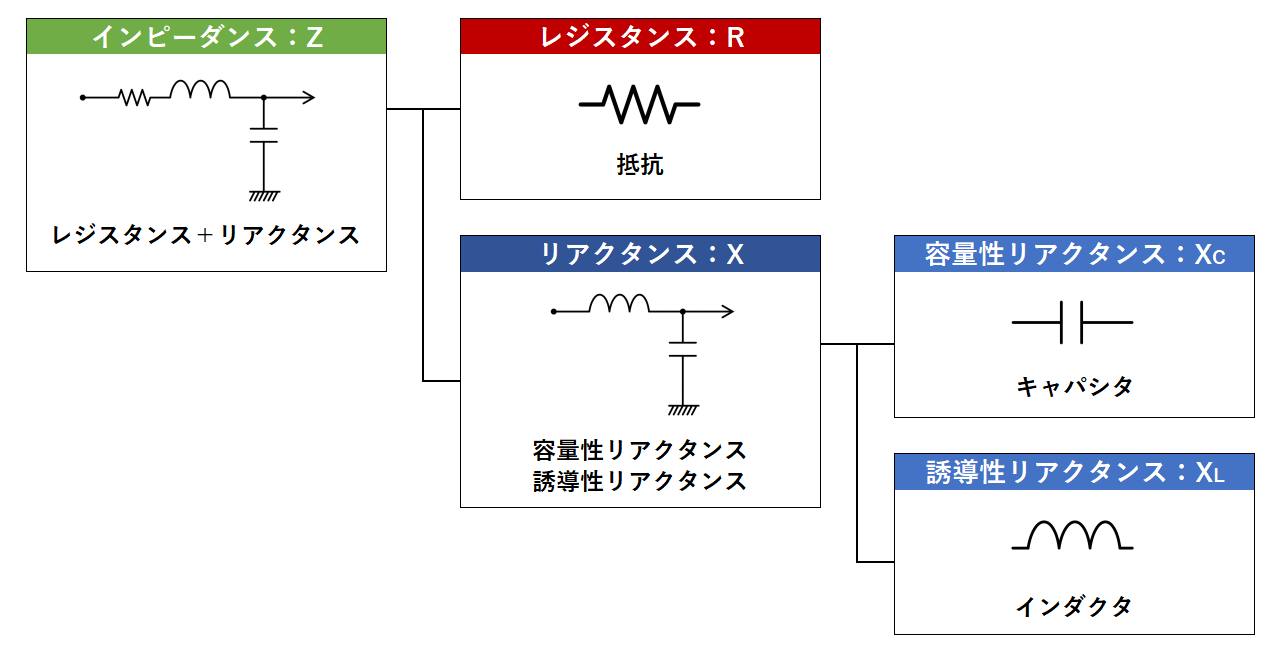
違いをまとめると以下のようになります。
| 項目 | 定義 |
|---|---|
| 抵抗(レジスタンス) | 電流の流れを妨げるもののうち、周波数によって値が変化しないもの |
| リアクタンス | 電流の流れを妨げるもののうち、周波数によって値が変化するもの容量性リアクタンスと誘導性リアクタンスを合わせたもの |
| インピーダンス | 抵抗とリアクタンスを合わせたもの |
インピーダンスは、抵抗やコンデンサ、コイルといった特定の部品ではなく、接続される回路(負荷)の電流の流れにくさを表します。
入力側から見た負荷側のインピーダンスを負荷インピーダンスという呼び方をします。
次に、少し分かりにくいリアクタンスについて詳しく説明していきます。
リアクタンスとは
リアクタンスとは、キャパシタ(コンデンサ)やインダクタ(コイル)における電流の流れにくさです。
交流回路でキャパシタによる電流の流れにくさを容量性リアクタンスと呼び、インダクタによる電流の流れにくさを誘導性リアクタンスと呼びます。
容量性リアクタンス
容量性リアクタンスは、
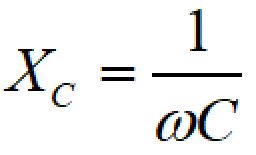
で表されます。ωは角周波数で、
Cはコンデンサの容量、fは入力信号の周波数です。
容量性リアクタンスは周波数に反比例するため、高周波になるほど小さくなることが分かります。
コンデンサのインピーダンス
コンデンサのインピーダンスは下記の式で表されます。
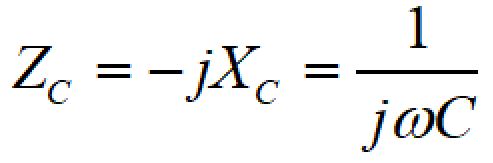
jは虚数単位です。
なぜ虚数を用いた複素数で表されるのかを解説していきます。
コンデンサにサイン波を印加すると、入力電圧に対しコンデンサに流れる電流は1/4波長(=90度)位相が進みます。
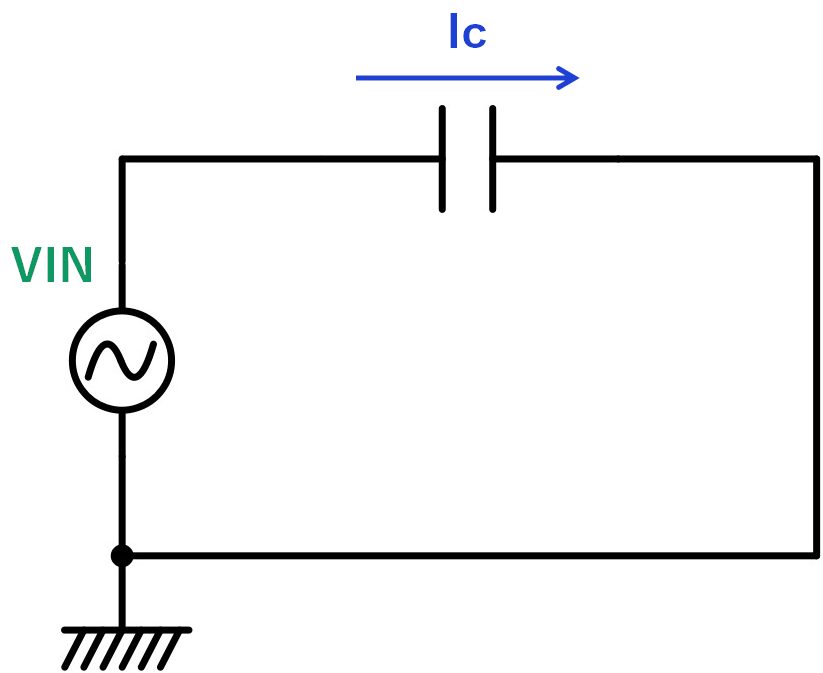
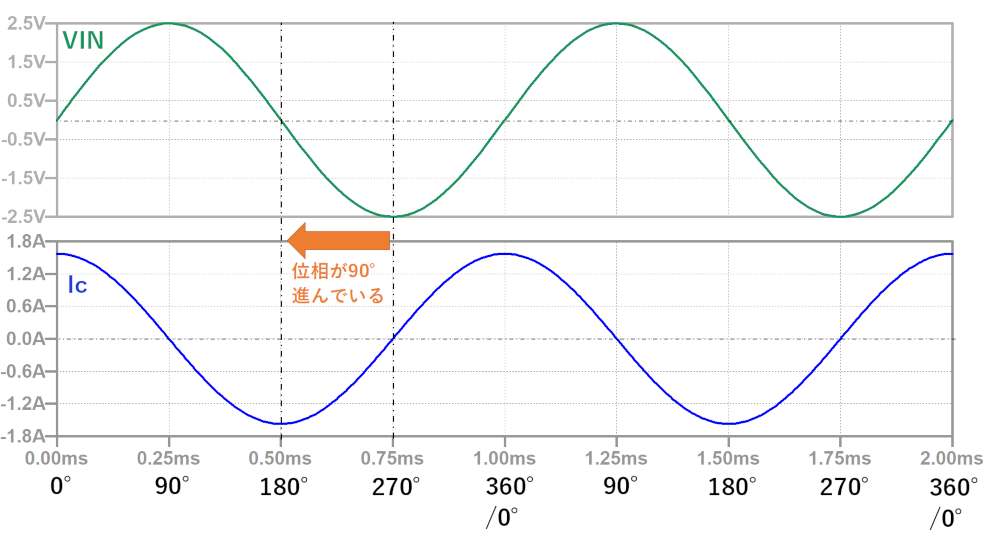
この位相のズレを数式で表すために複素数を使います。
90度位相が進んで、大きさがXcのインピーダンスを極座標で表すの下図のようになります。
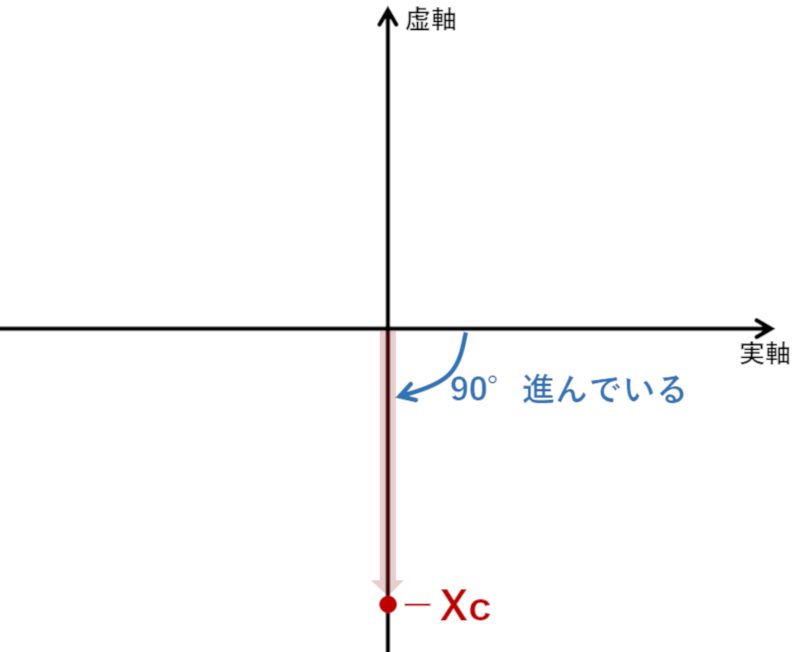
これを数式で表すと、
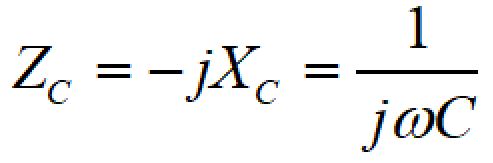
となるのです。
誘導性リアクタンス
誘導性リアクタンスは、
で表されます。Lはコイルのインダクタンスです。
誘導性リアクタンスは周波数に比例するため、高周波になるほど大きくなることが分かります。
インダクタのインピーダンス
インダクタのインピーダンスは下記の式で表されます。
インダクタにサイン波を印加すると、入力電圧に対しコンデンサに流れる電流は1/4波長(=90度)位相が遅れます。
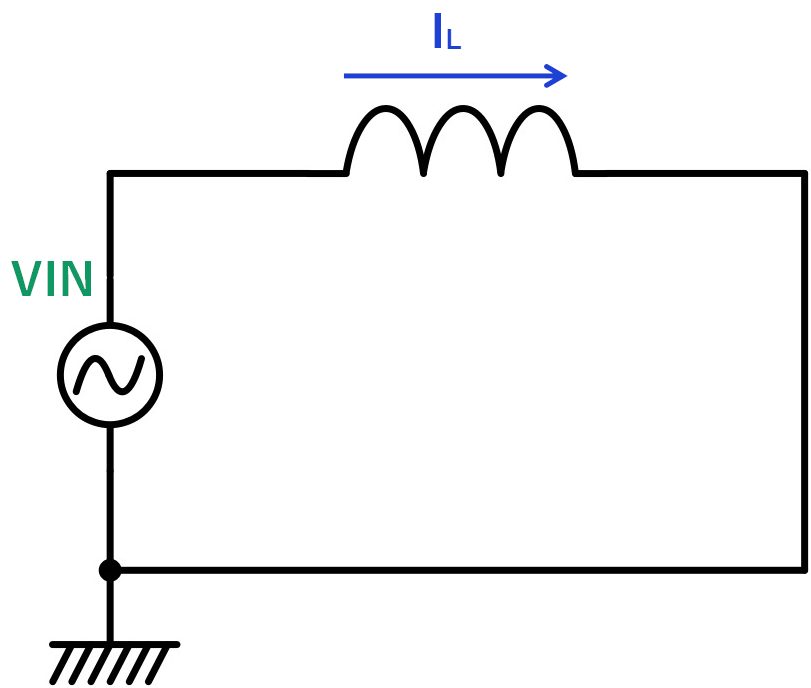
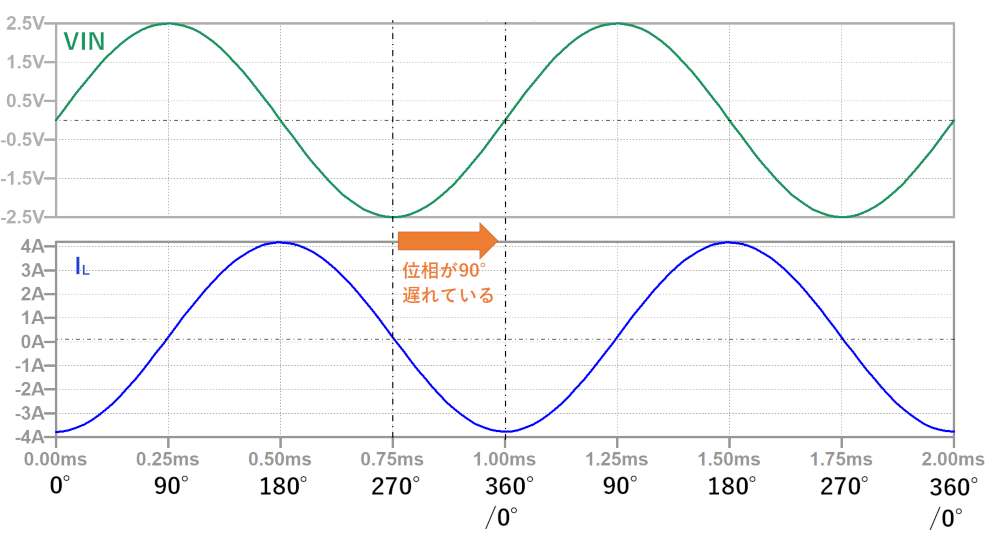
コンデンサの時と同様に、極座標で表すと下図のようになります。
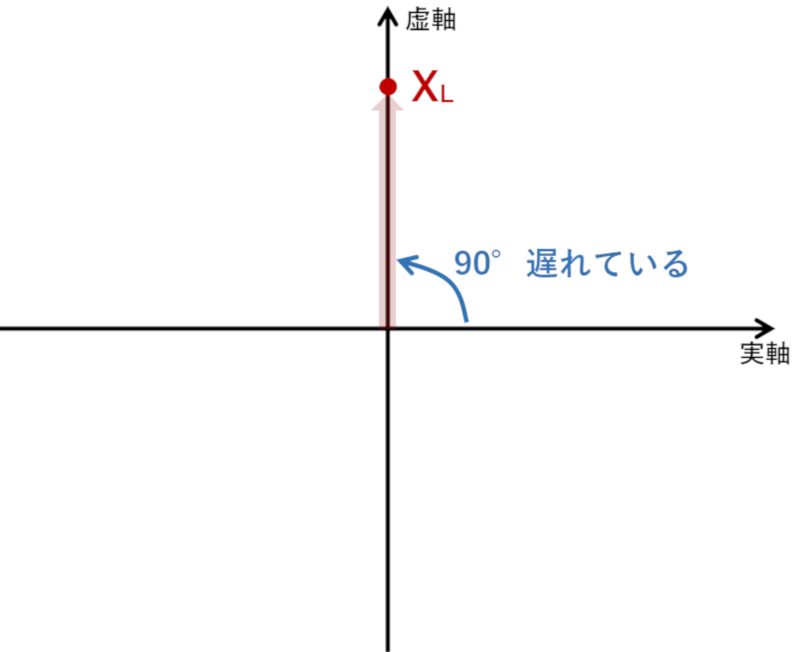
これを数式で表すと、
となるのです。
インピーダンスの計算方法
以下の3つの回路例を挙げて、インピーダンスの計算方法を説明していきます。
- RCローパスフィルタ
- RLハイパスフィルタ
- RLCバンドパスフィルタ
1.RCフィルタのインピーダンスの求め方
下図のようなRCローパスフィルタを考えます。
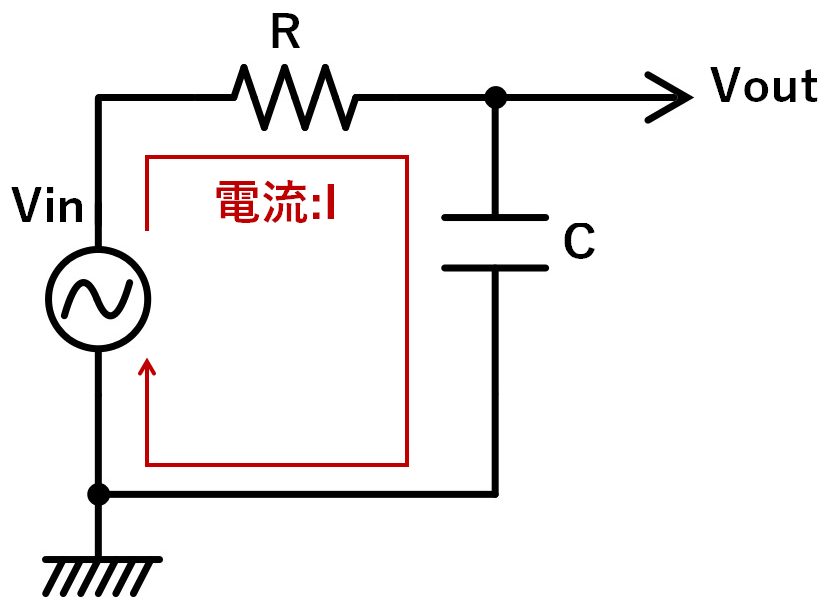
入力側から見ると、RCは直列に接続されているため、合成インピーダンスは、
となります。
これはベクトルになりますので、電流値を計算するためにスカラ量(絶対値)に変換してインピーダンスの大きさを求めます。
ベクトルの絶対値は三平方の定理より、
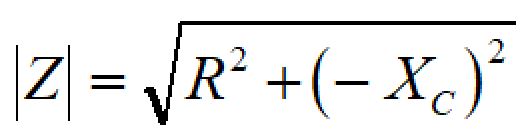
となります。
よって、電流:Iは、
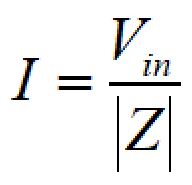
で求められます。
また、位相のずれは、
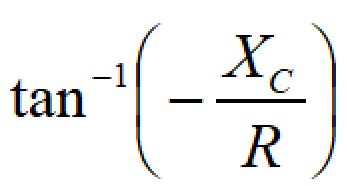
で計算できます。
計算例
R=1kΩ、C=0.1uF、Vin=±2.5V / 1kHzの条件で考えます。
この条件で、リアクタンス、合成インピーダンス、電流値を求めると、
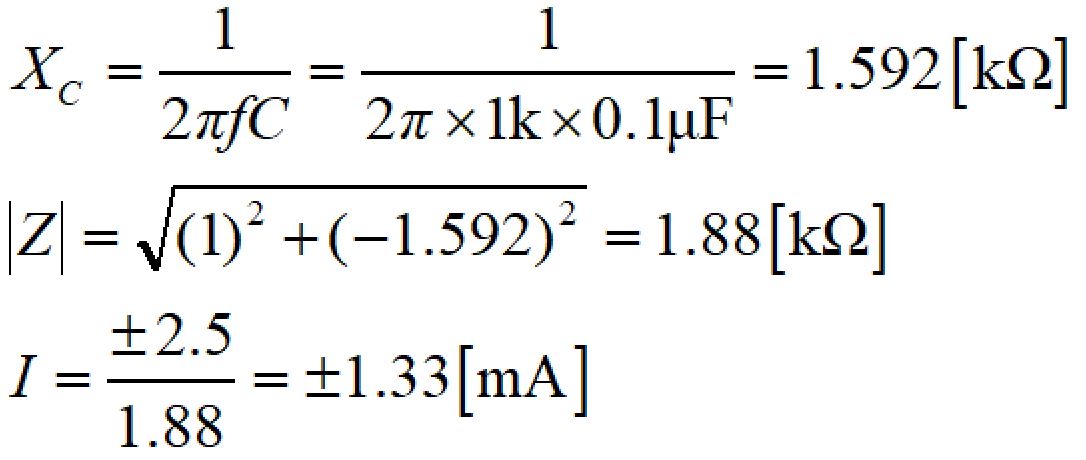
位相進みは、
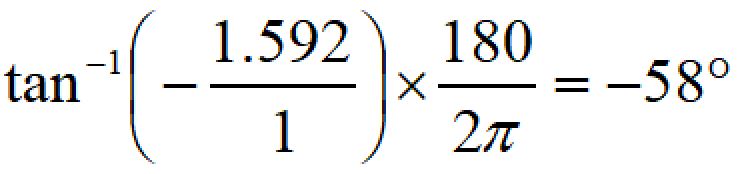
となります。
下図がシミュレーション結果です。
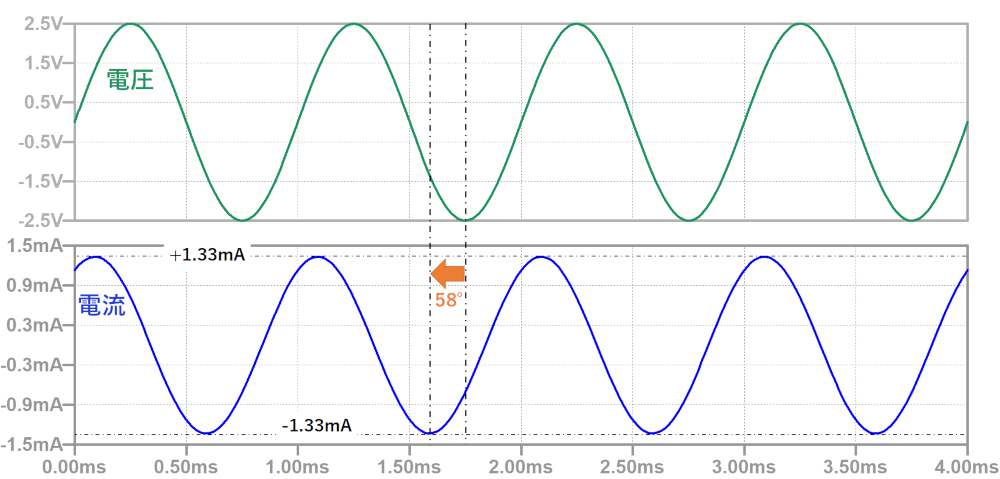
2.RLフィルタのインピーダンスの求め方
下図のようなRLハイパスフィルタを考えます。
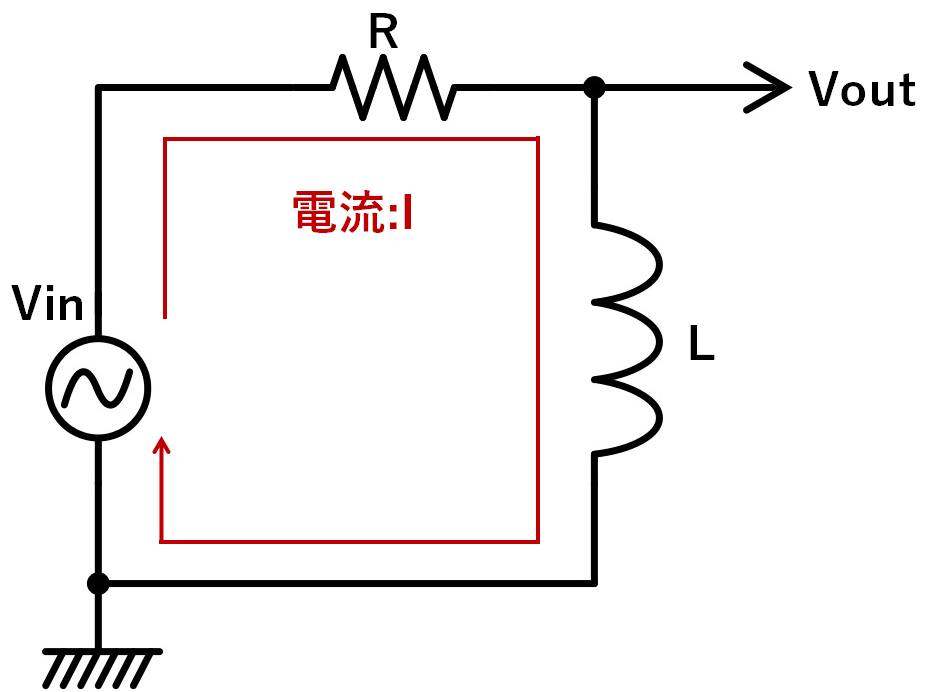
入力側から見ると、RLは直列に接続されているため、合成インピーダンスは、
となります。
絶対値を取ってインピーダンスの大きさを求めると、
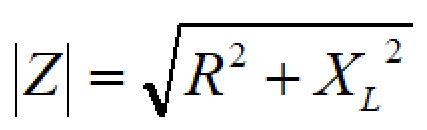
よって、電流:Iは、
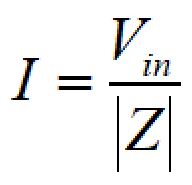
となります。
位相遅れは、
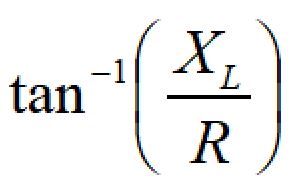
で計算できます。
計算例
R=30Ω、L=100uH、Vin=±2.5V / 100kHzの条件で考えます。
この条件で、リアクタンス、合成インピーダンス、電流値を求めると、
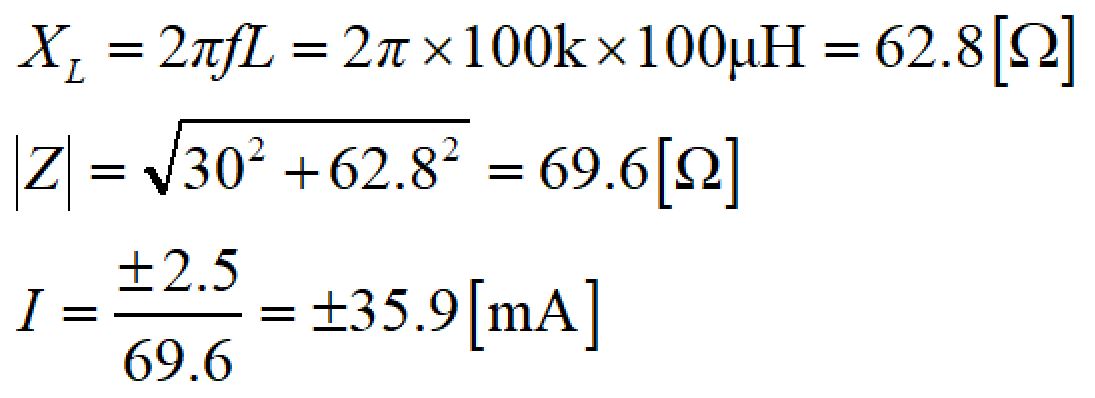
位相遅れは、
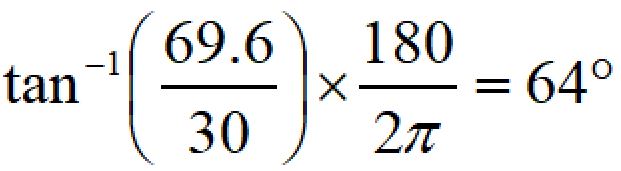
となります。
下図がシミュレーション結果です。
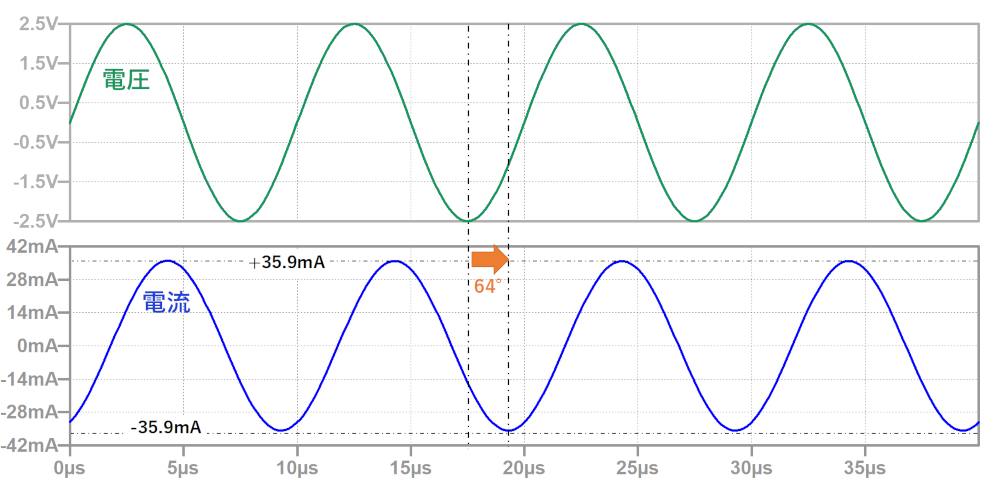
3.RLCフィルタのインピーダンスの求め方
下図のようなRLCバンドパスフィルタを考えます。
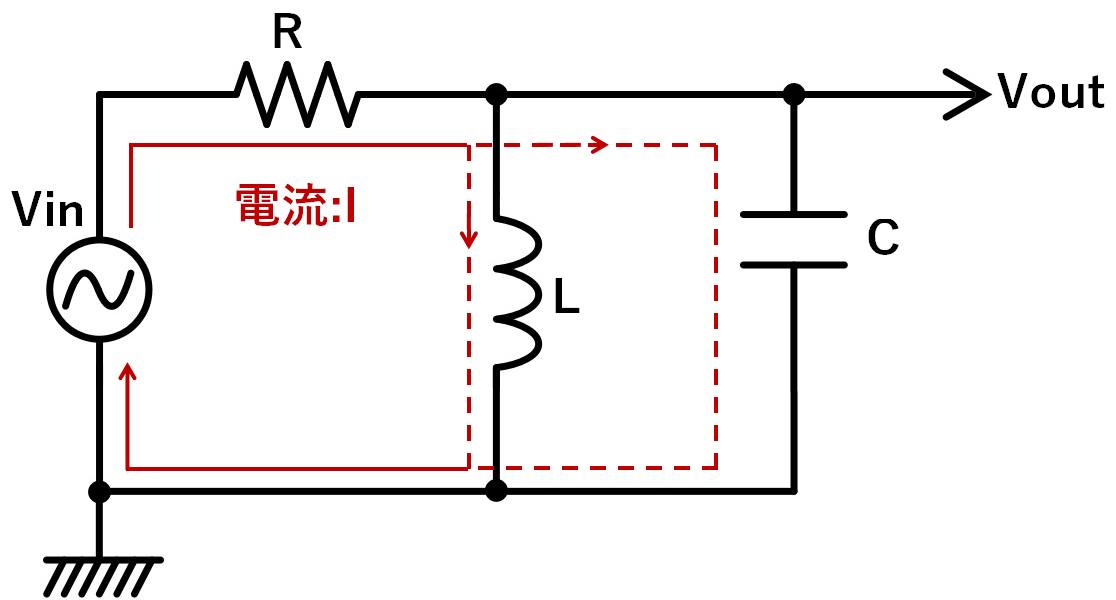
入力側から見ると、RとLCの合成リアクタンスが直列に接続されています。
まず、LCの合成リアクタンスを計算します。
LCは並列に接続されているので、
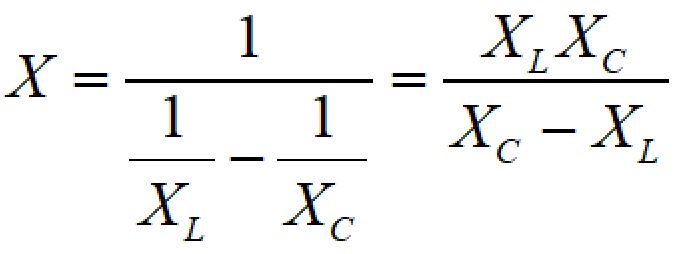
となります。
抵抗とリアクタンスの合成インピーダンスは、
絶対値を取ってインピーダンスの大きさを求めると、
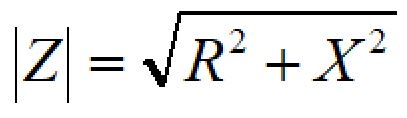
よって、電流:Iは、
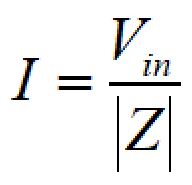
となります。
位相遅れは、
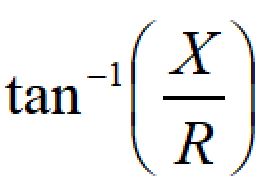
で計算できます。
計算例
R=30Ω、L=100uH、C=0.01uF、Vin=±2.5V / 100kHzの条件で考えます。
この条件で、リアクタンス、合成インピーダンス、電流値を求めると、
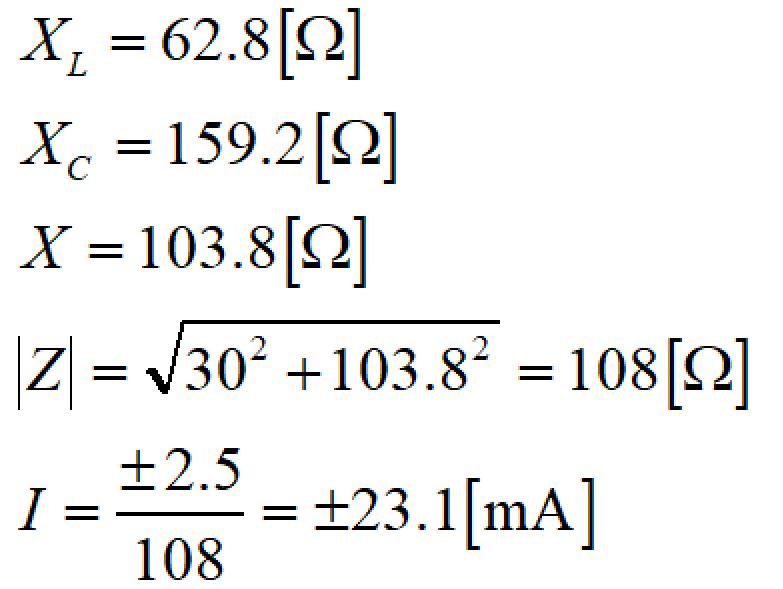
となります。
位相遅れは、
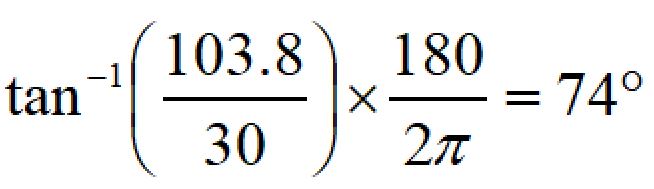
となります。
下図がシミュレーション結果です。
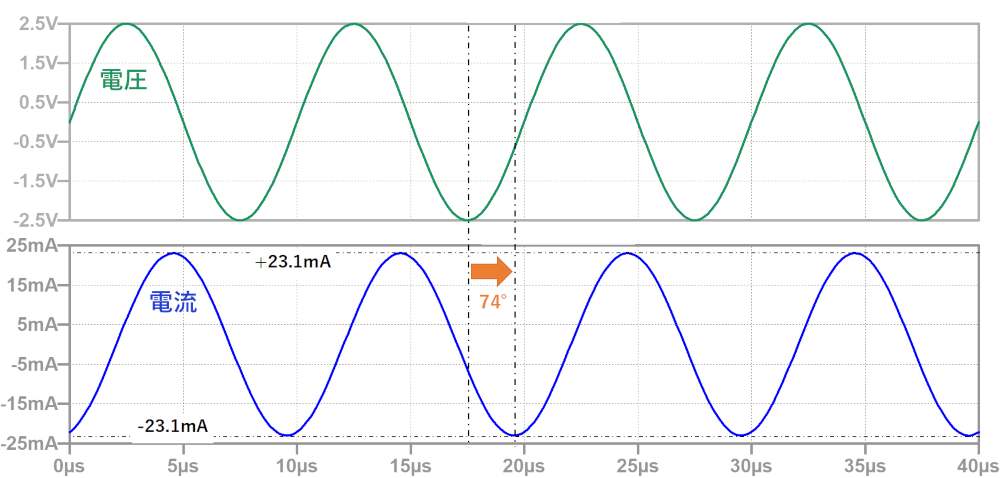
Analogistaでは、電子回路の基礎から学習できるセミナー動画を作成しました。
電子の動きをアニメーションを使って解説したり、シミュレーションを使って回路動作を説明し、直感的に理解しやすい内容としています。
これから電子回路を学ぶ必要がある社会人の方、趣味で電子工作を始めたい方におすすめの講座になっています。