サレンキー型2次フィルタの特性と設計計算
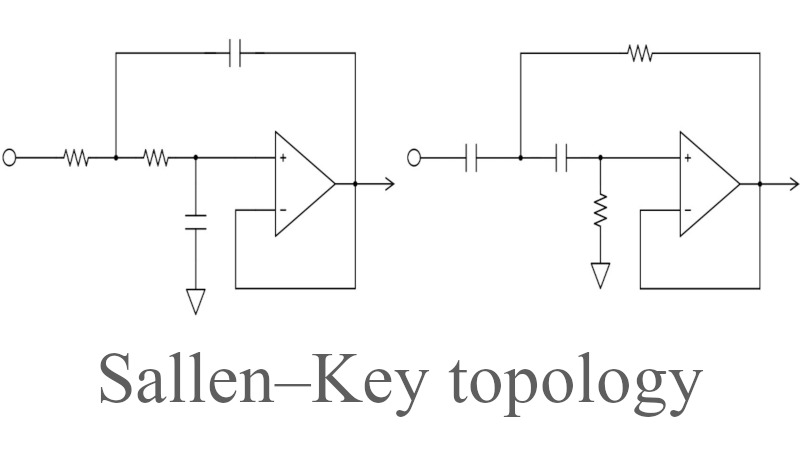
サレンキー(Sallen-Key)型フィルタとは、VCVS型(電圧制御電圧源型)アクティブフィルタを構成する方法です。
本稿では、サレンキー型の2次ローパスフィルタ、ハイパスフィルタの設計方法や特性について解説していきます。
2次ローパスフィルタ(LPF)
サレンキー型の2次ローパスフィルタはこのような回路です。
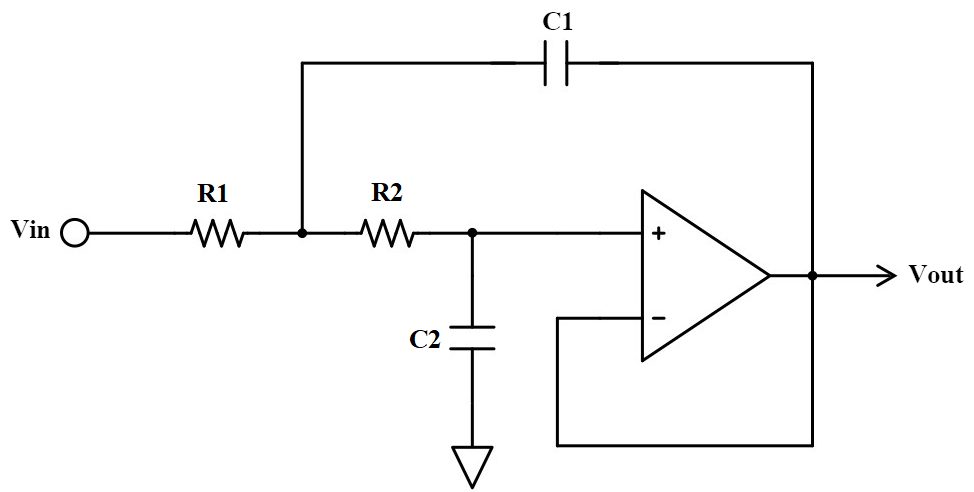
伝達関数、カットオフ周波数、Q値は以下の式で表されます。
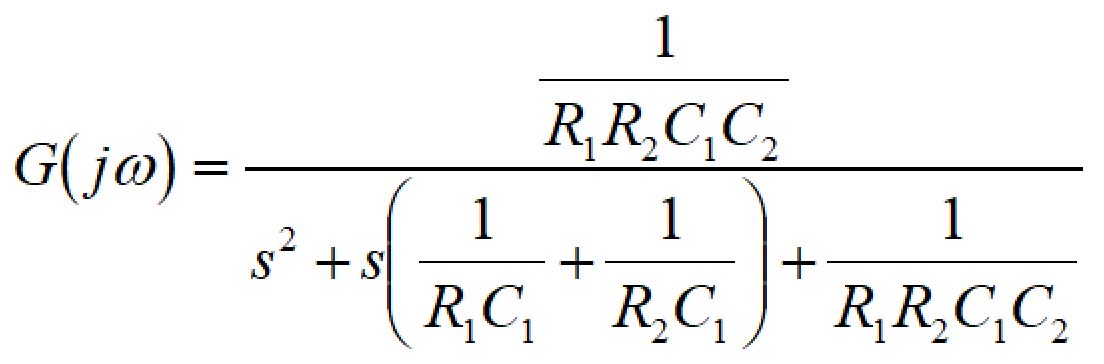
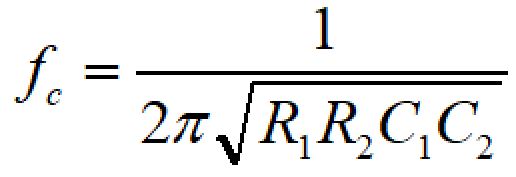
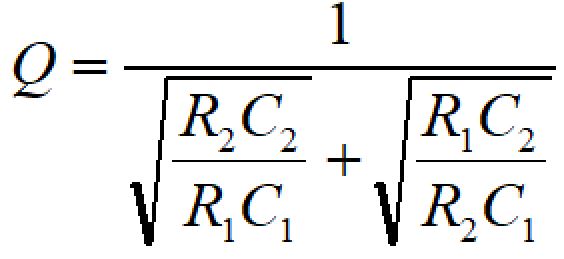
設計計算
計算を簡単にするため、R1=R2=Rとすると、
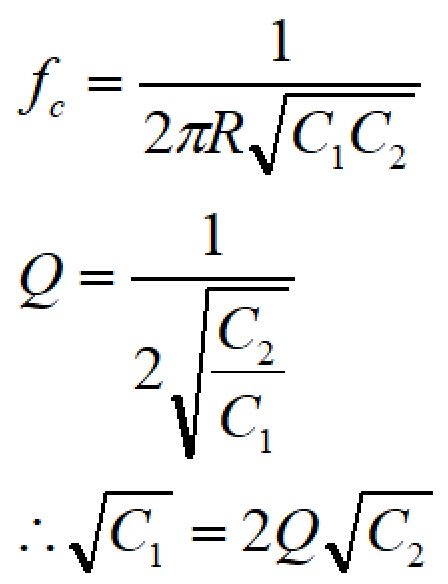
となります。
カットオフ周波数fcに√C1を代入すると、
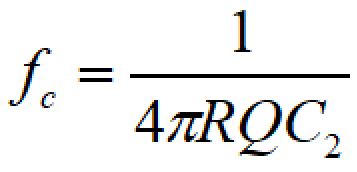
これより、C1、C2を求めると、
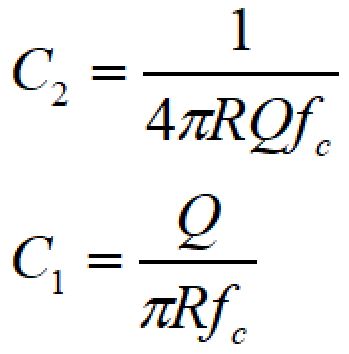
となり、カットオフ周波数とQ値を決めればC1、C2の値を計算できます。
例えば、R1=R2=10kΩ、Q値を1とすれば、
C1=31.8nF、C2=8.0nFと計算できます。
周波数特性
下図の回路で、R1=R2=10kΩ、カットオフ周波数=1kHzとして、Q値を振った場合の周波数特性をLTspiceで確認してみます。
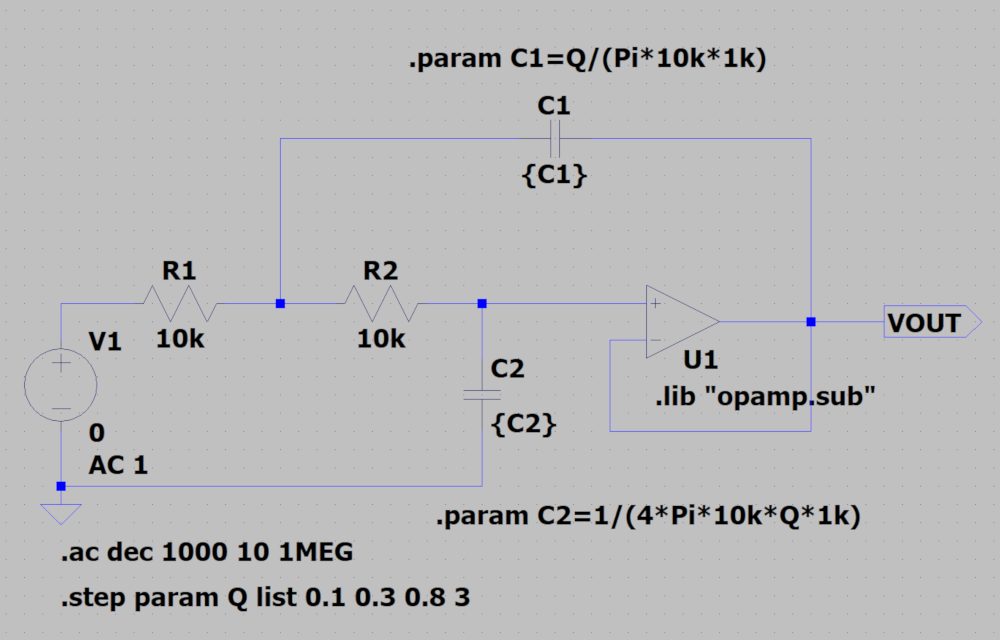
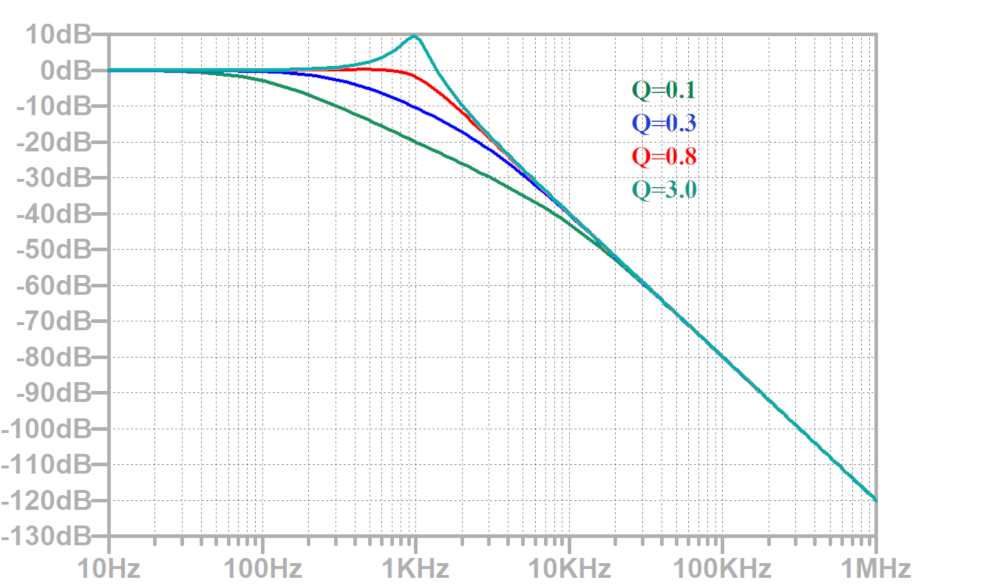
減衰特性は-40dB/decadeとなっていることが分かります。
増幅する場合
先述の回路ではオペアンプがボルテージフォロワ型になっているため、増幅作用はありません。
下図のように非反転増幅型にすることで、増幅することができます。
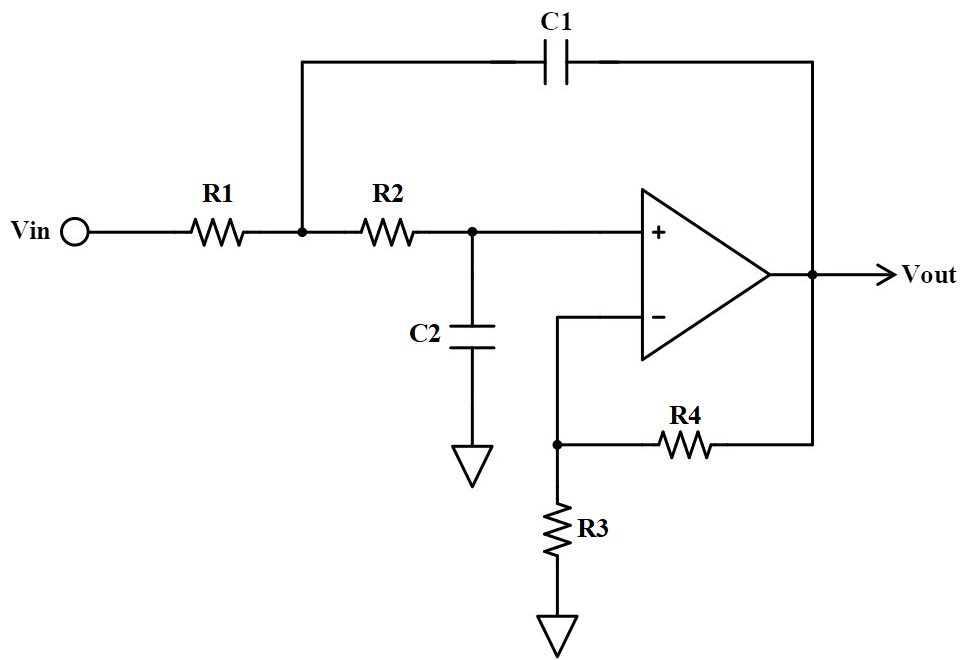
増幅率は、
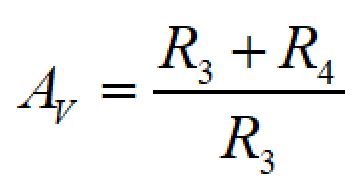
で計算できます。
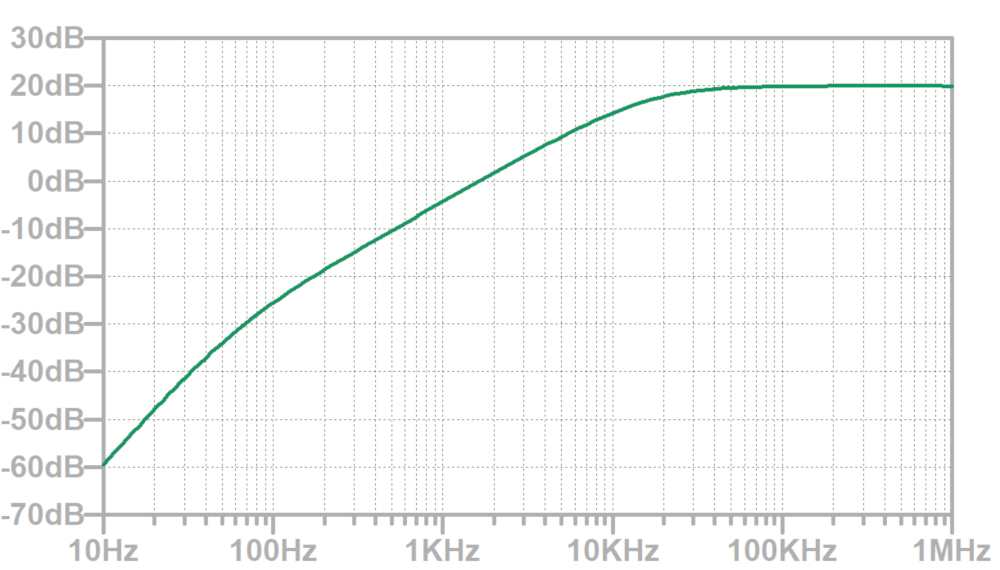
下図の条件でシミューレーションを行うと、カットオフ周波数以下ではゲインが20dB(10倍)となっていることが分かります。
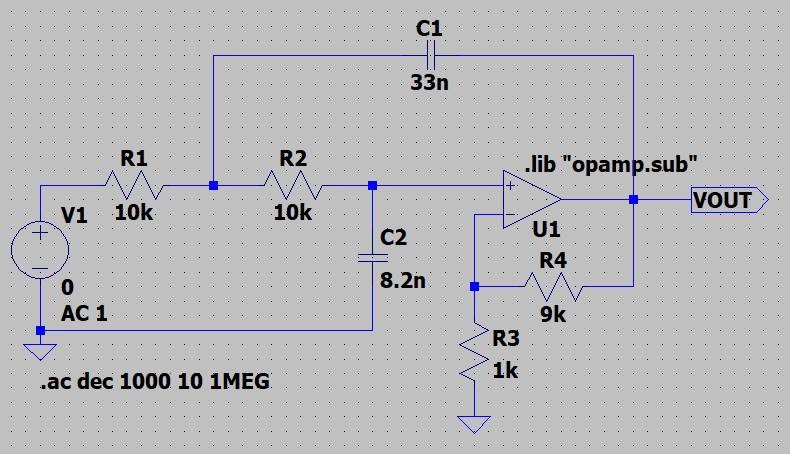
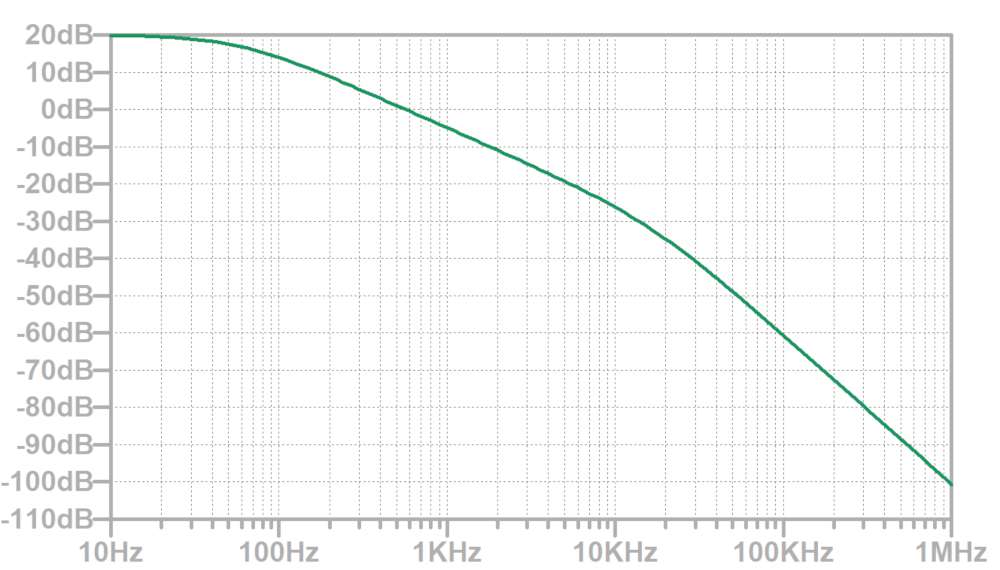
2次ハイパスフィルタ(HPF)
サレンキー型の2次ハイパスフィルタはこのような回路です。
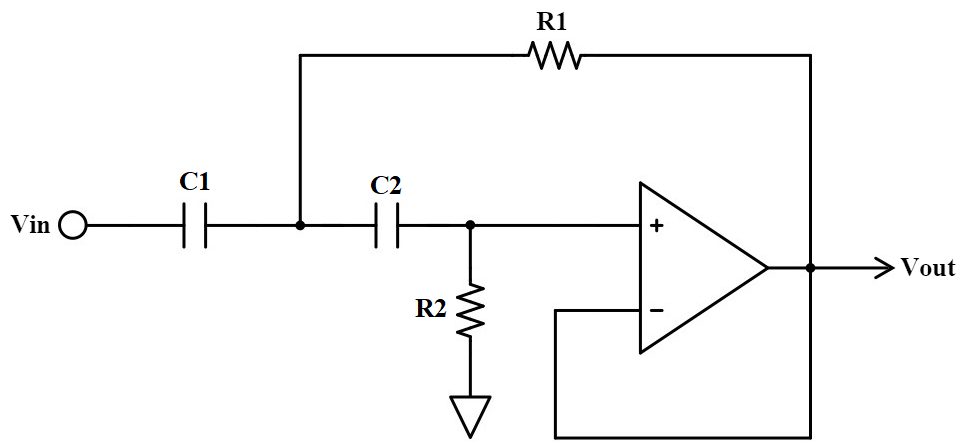
伝達関数、カットオフ周波数、Q値は以下の式で表されます。
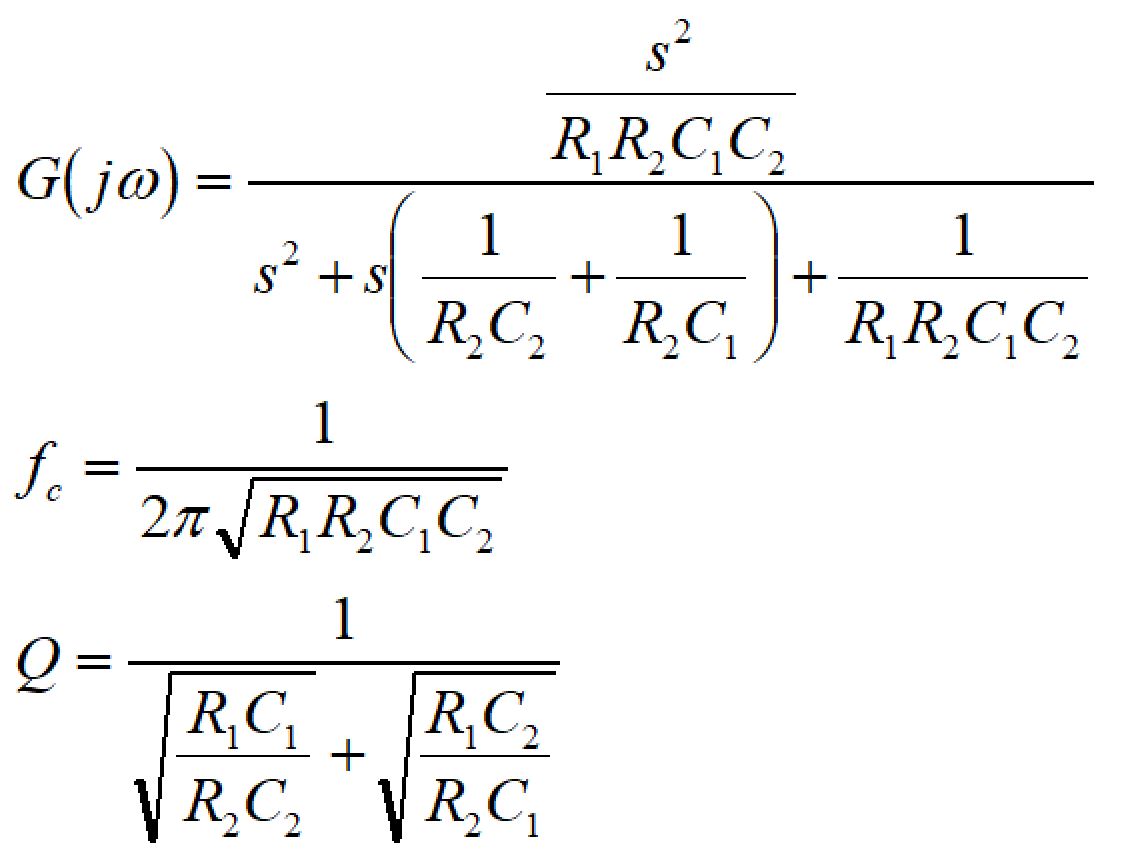
設計計算
計算を簡単にするため、C1=C2=Cとすると、
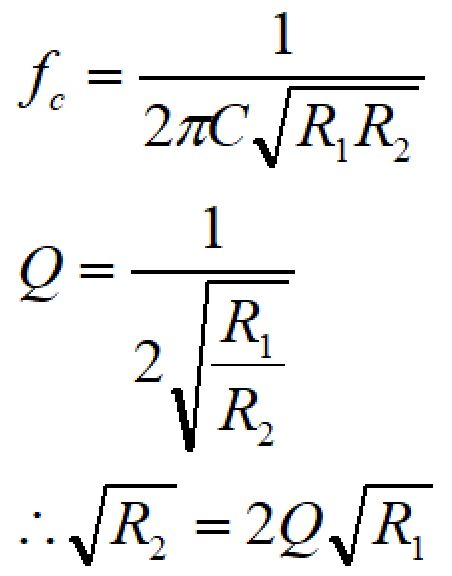
となります。
カットオフ周波数fcに√R2を代入すると、
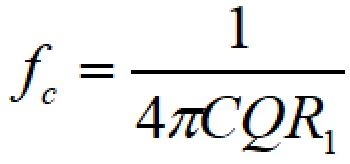
これより、R1、R2を求めると、
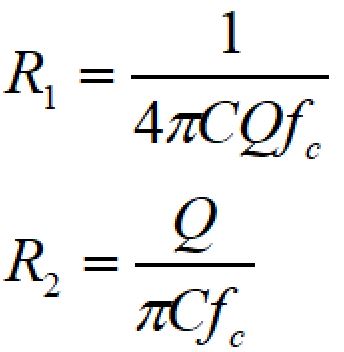
となり、カットオフ周波数とQ値を決めればR1、R2の値を計算できます。
例えば、C1=C2=10nF、Q値を1とすれば、
R1=8kΩ、R2=32kΩと計算できます。
周波数特性
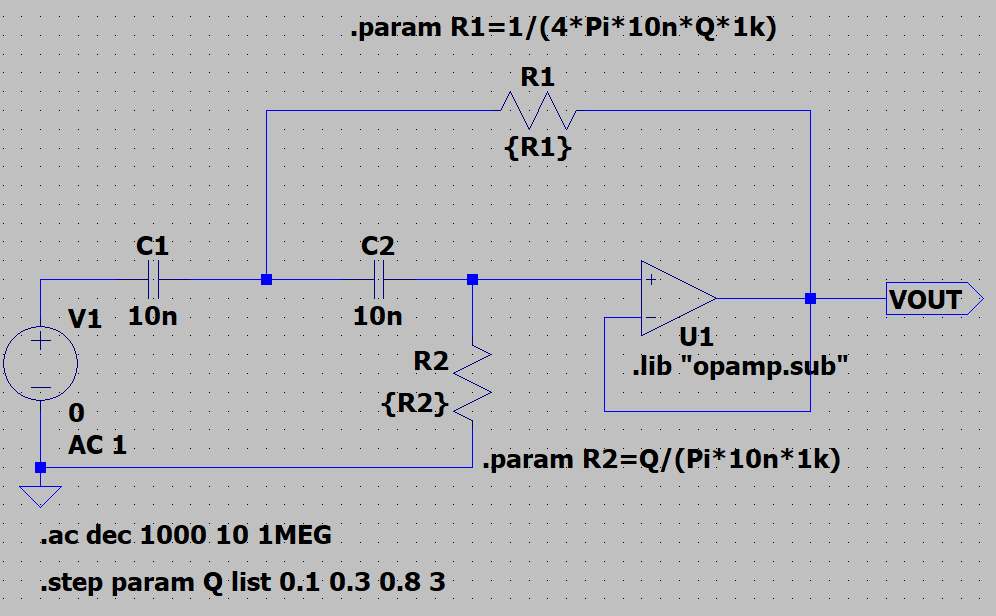
下図の回路で、C1=C2=10nF、カットオフ周波数=1kHzとして、Q値を振った場合の周波数特性をLTspiceで確認してみます。
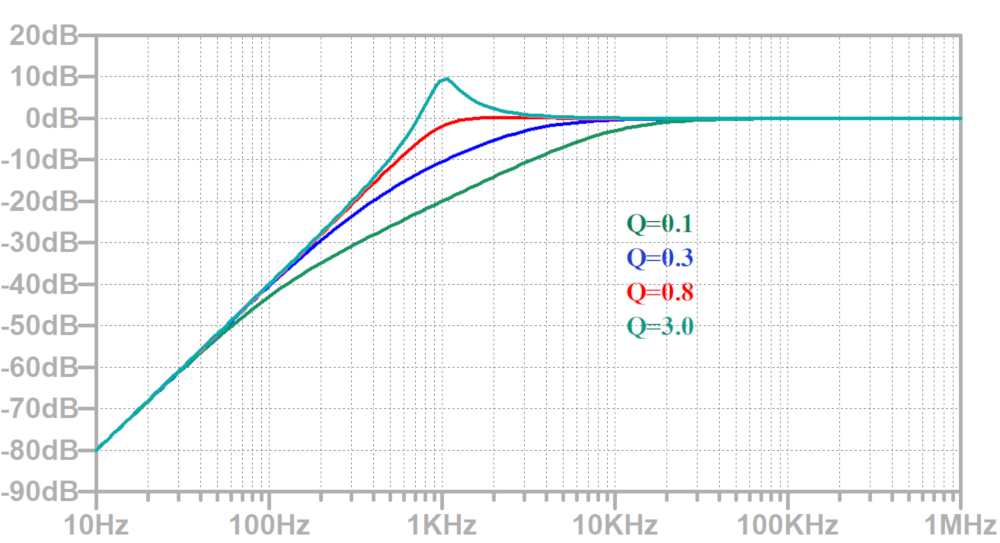
減衰特性は-40dB/decadeとなっていることが分かります。
増幅する場合
ローパスフィルタの場合と同様に、非反転増幅型にすることで増幅することができます。
下図の回路でシミュレーションを行います。
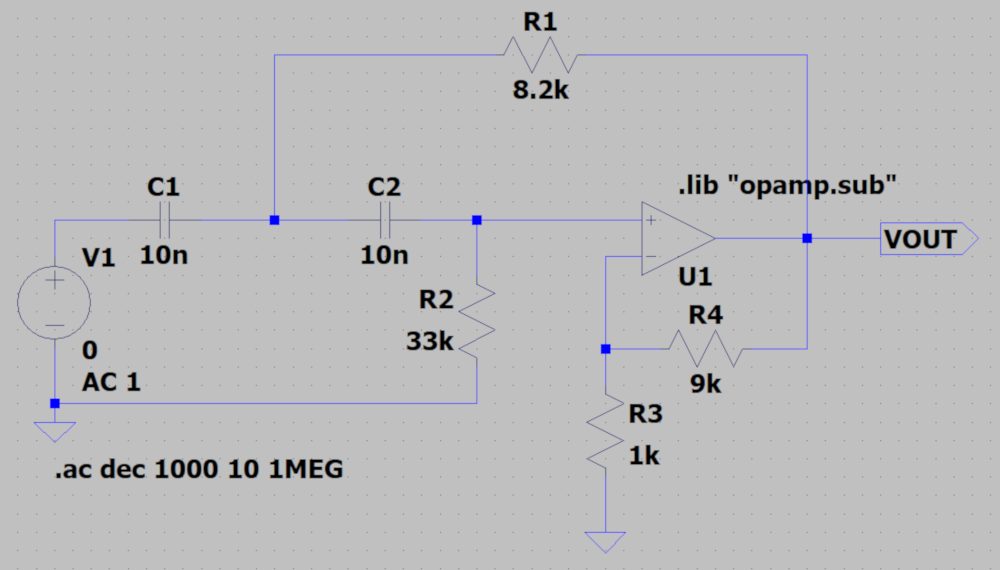
カットオフ周波数以上ではゲインが20dB(10倍)となっていることが分かります。