電流帰還バイアス回路の原理と設計計算の方法
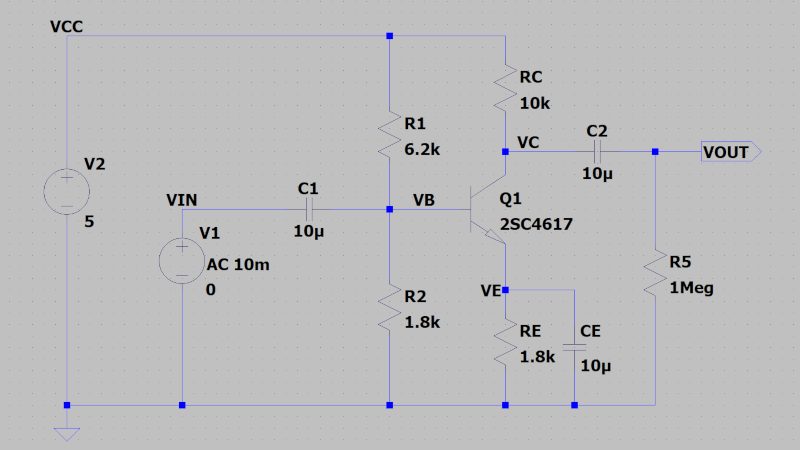
電流帰還バイアス回路とは、エミッタ抵抗によって負帰還(フィードバック)を構成し、ベース電流(バイアス電流)を制御することができる増幅回路です。
エミッタ接地回路と比べ電圧利得は下がるが、周波数特性、ノイズ、歪みが改善し、温度変化によるばらつきも抑えられます。
本稿では、電流帰還バイアス回路の動作原理と設計方法について解説します。
回路図構成
エミッタ接地回路のエミッタ側に抵抗を入れた形となります。
それだけだと増幅率が大きく低下してしまいますので、エミッタ抵抗と並列にコンデンサを入れます。
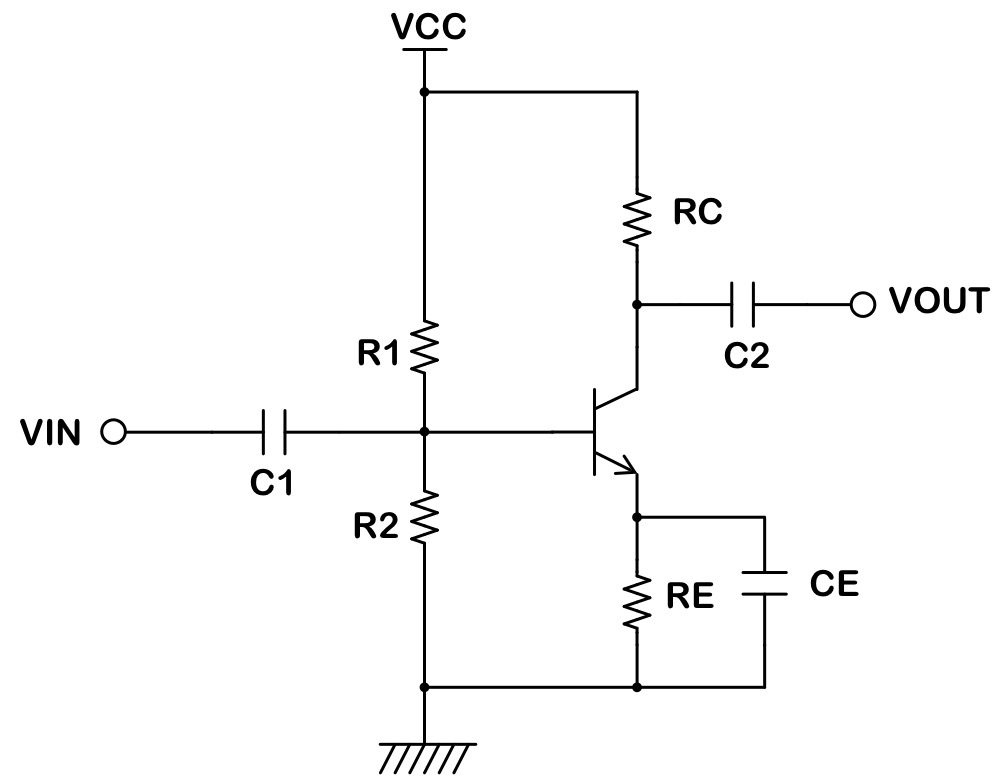
コンデンサによって、AC的にはエミッタがGNDショート状態に見えるので、高い増幅率が得られます。
動作原理
まず、DC特性(静特性)を考えます。
温度上昇すると、トランジスタのhFEは大きくなり、コレクタ電流が増加します。
しかし、エミッタ抵抗によりエミッタ電圧も大きくなり、VBEを小さくする方向に作用します。
結果、ベース電流が低下し、温度上昇によるコレクタ電流の変化が抑えられることになります。
つまり、エミッタ抵抗によって負帰還が働き、動作点を安定させることができるのです。
次に、AC特性を考えます。
CEはハイパスコンデンサとして働き、カットオフ周波数以上の帯域ではエミッタがGNDにショートされている状態となるため、エミッタ抵抗による負帰還が働かず高い増幅率が得られます。
カットオフ周波数:fcは、エミッタを出力と見た場合の出力インピーダンス:ZEOとCEで決まります。
(※ZEO << REとする)
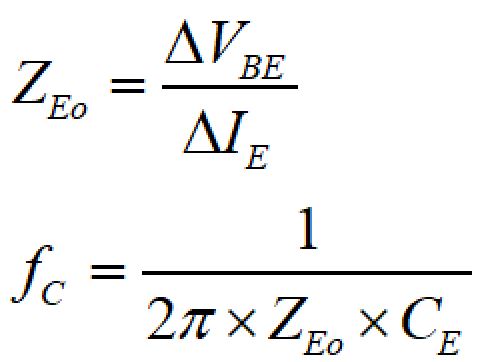
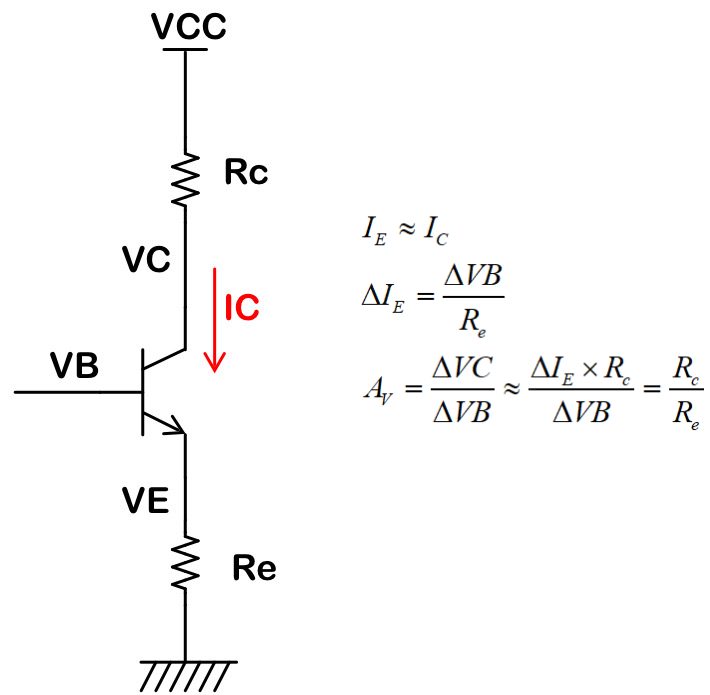
増幅率:Avは、
で計算できます。
CEが無い場合の増幅率はコレクタ抵抗とエミッタ抵抗の比だけで決まり、
Av = RC / RE
となります。
設計計算
実際に使う場合、エミッタ抵抗を分割し、その中点にコンデンサを接続します。
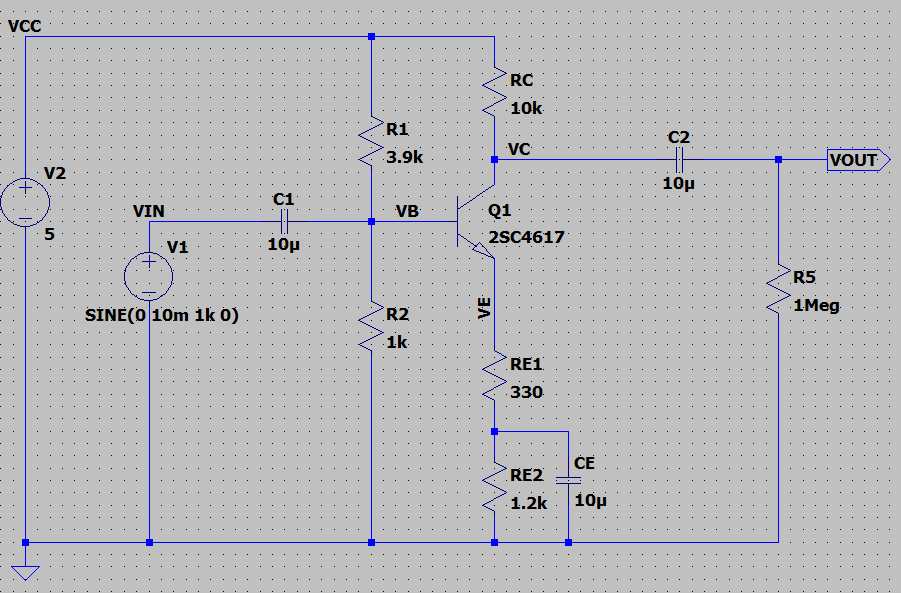
こうすることで、DC的な帰還量はRE1+RE2で決めることができ、AC的な増幅率はRE1で決めることができるため、帰還量を大きく取っても増幅率を下げなくてもよくなります。
また、RCとRE1で増幅率がほぼ決まるので、トランジスタのばらつきによる影響を抑えることができます。
増幅率が33倍を狙って回路を設計します。
入力振幅が最大±10mVとすると、出力振幅は±330mVとなります。
コレクタ電圧の上限、下限に余裕を持たせて、動作点は2Vとします。
VCCは5V、コレクタ抵抗:RCを10kΩとすると、コレクタ電流は、
IC = ( 5V – 2V ) / 10kΩ = 300uA
となります。
コレクタ電圧の下限は2V – 330mV = 1.67V
エミッタ抵抗の合計値はトランジスタが飽和しないように設定する必要があります。
エミッタ抵抗を1.53kΩとしているので、エミッタ電圧は、
VE = 300uA × 1.53kΩ = 459mV
となり、VCEは十分確保できています。
IC=300uAを出力するのに必要なVBEを、VBE-IC特性から確認すると、573mVであることが分かります。
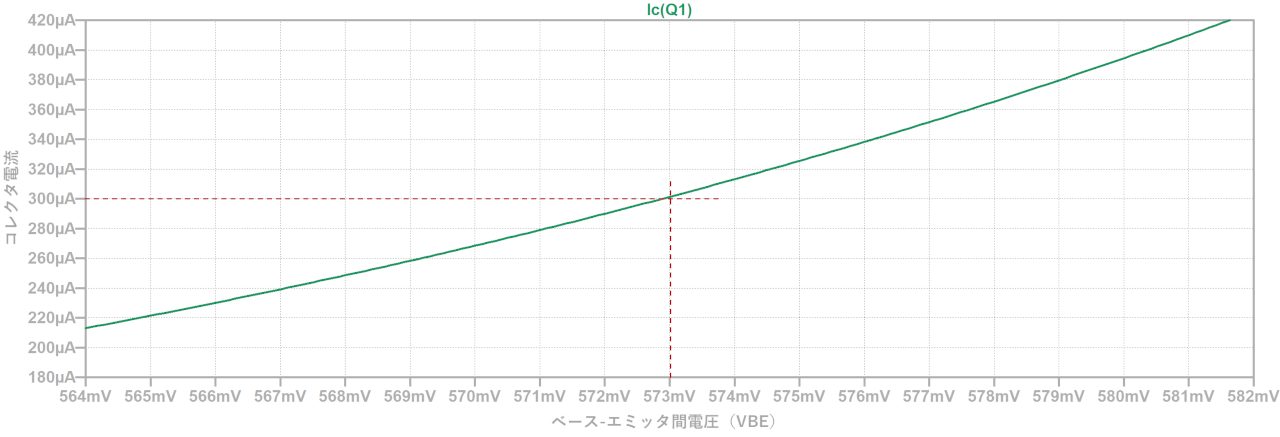
したがって、バイアス電圧は、459mV + 573mV = 1.032Vとする必要があります。
今回の設定では、ベース電流は数uA程度なので、数kΩオーダーの抵抗値を選べば、ベース電流の影響を無視してブリーダー抵抗:R1、R2の比だけでバイアス電圧を決めることができます。
バイアス電圧:VBは、
VB = VCC × R2 / ( R1 + R2 )
で計算できます。
R1=3.9kΩ、R2=1kΩを選定すると、VB=1.02Vとなります。
この回路でシミュレーションを行います。
入力信号は、±10mV、1kHzのサイン波です。
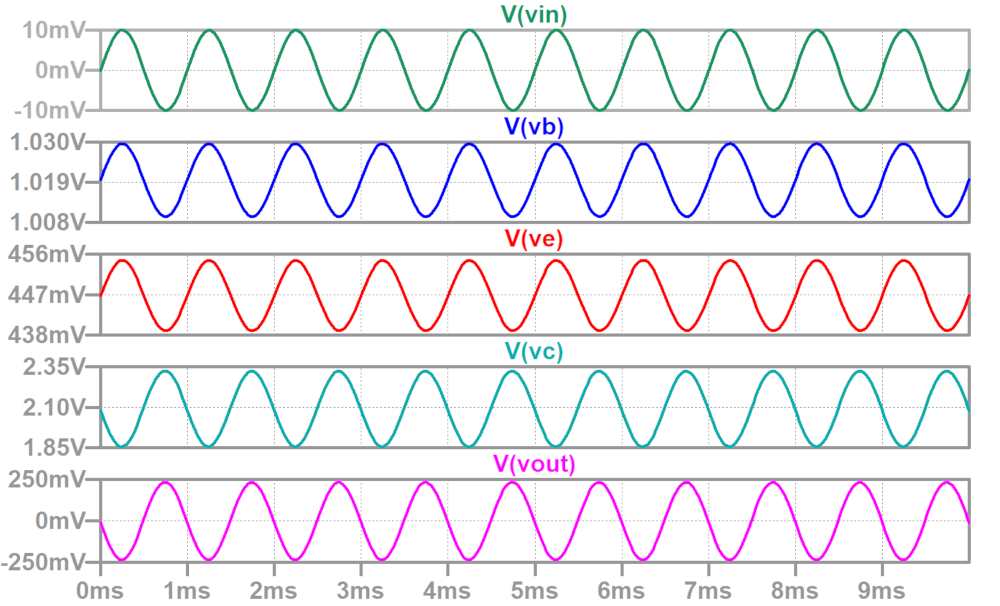
ほぼ設計通りの動作となっていることが確認できましたが、増幅率が25倍程度となっており、狙いより少し小さくなっています。
これは、トランジスタのベース-エミッタ間インピーダンスとRE1でエミッタの電圧が分圧されて減衰しているためです。
理想的にはVEの電圧振幅は入力と同じ±10mVとなりますが、上記波形では±7.8mVとなっています。
RE1の値が小さい(増幅率が高い)ほど、ベース-エミッタ間インピーダンスの影響が大きくなります。
周波数特性
前項で設計した電流帰還バイアス回路の周波数特性を確認します。
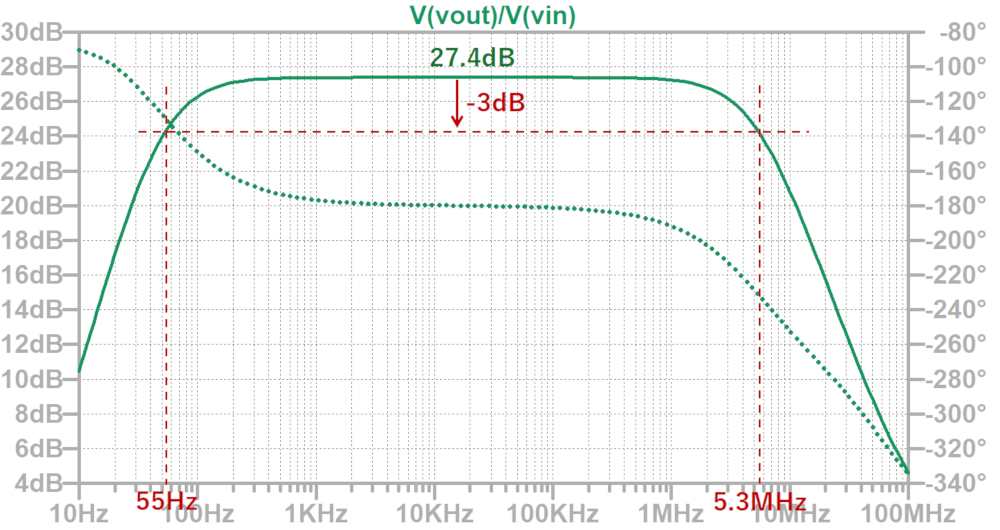
低周波側のカットオフ周波数(遮断周波数)は、CEとRE1で決まります。
また、CEとRE2はゼロを形成し、C1とR1とR2の合成抵抗によってポールが形成されます。
今回の場合、このポールとゼロはほぼ同じ周波数に形成されているため打ち消し合っています。
高周波側のカットオフ周波数はトランジスタの内部寄生容量によって決まります。
