オペアンプを使った微分回路の動作原理をシミュレーション波形を用いて解説
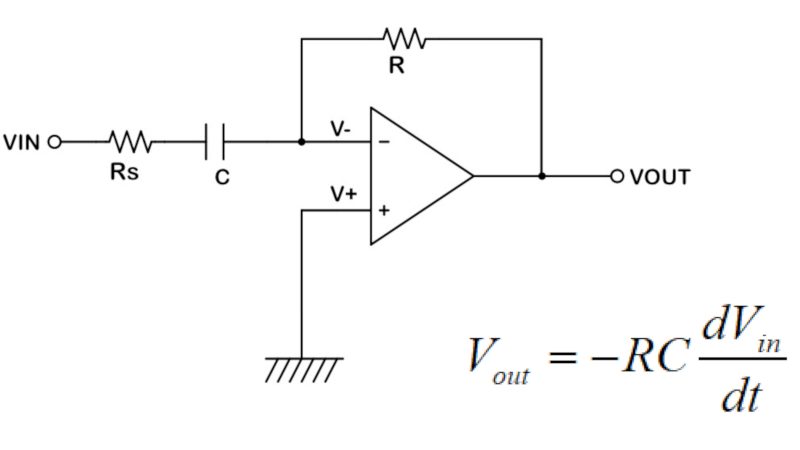
微分回路(微分器)とは、入力波形を時間微分した電圧(傾き)を出力する回路です。
微分回路の用途としてはハイパスフィルタやDC成分除去回路などがあります。
微分回路の原理
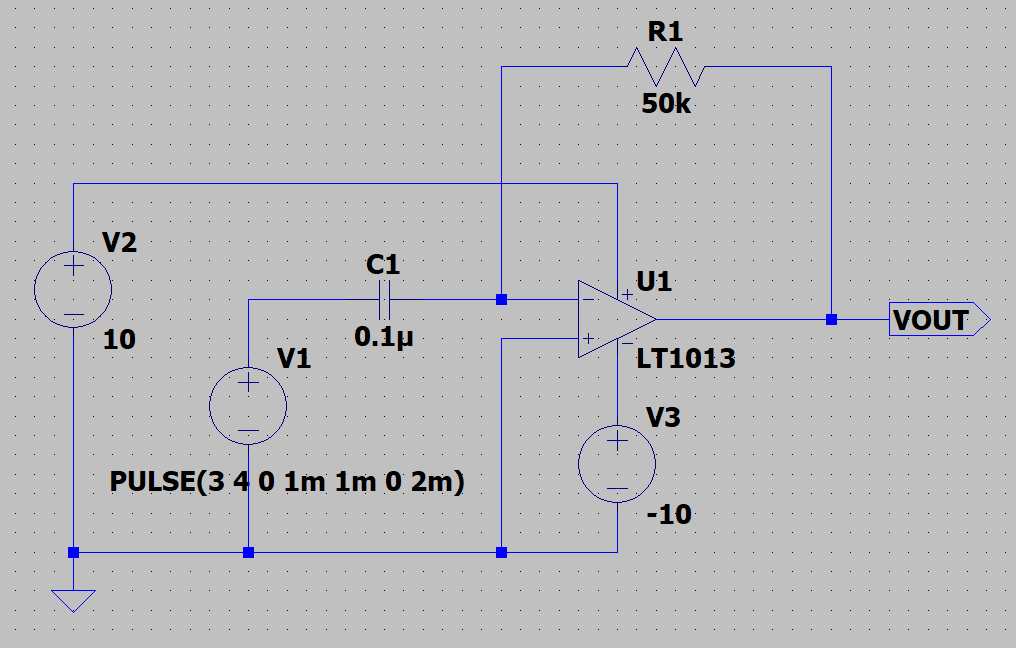
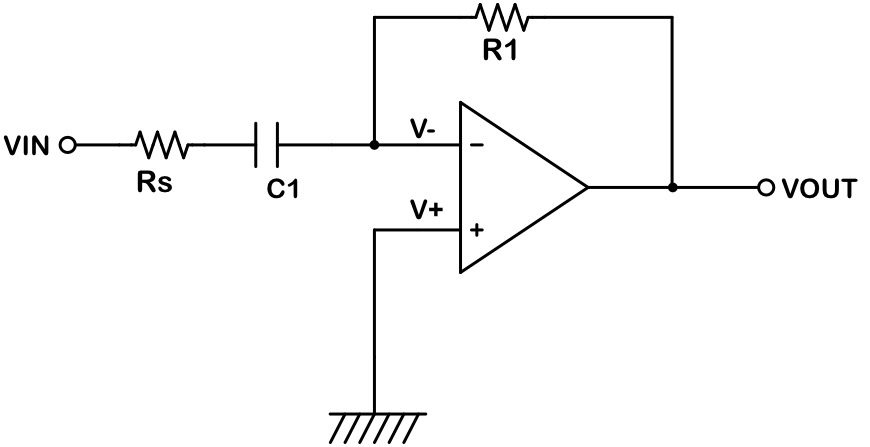
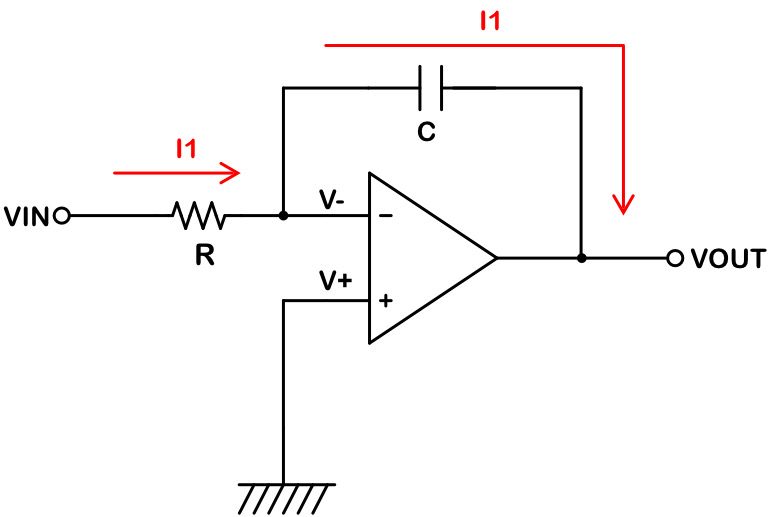
微分回路は、下図のように反転増幅器の入力側の抵抗をコンデンサに置き換えた回路になります。
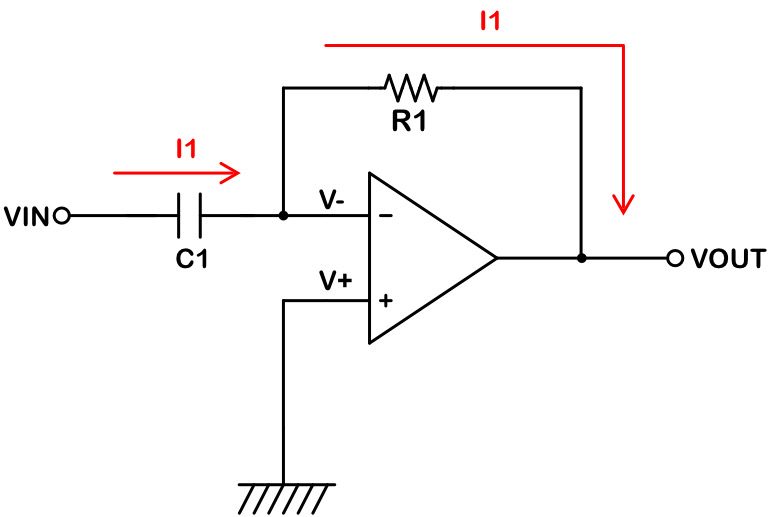
出力電圧の計算方法も、基本的には反転増幅器と同じ考え方になります。
バーチャルショートの考え方から、V+ = V- となります。
コンデンサにかかる電圧と電流の基本関係式から、I1は以下の式で計算できます。
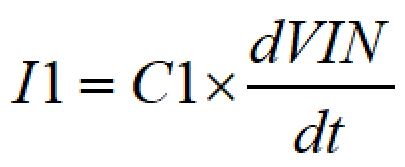
R1とI1による電圧降下より、微分回路の出力電圧の方程式は下記のようになります。
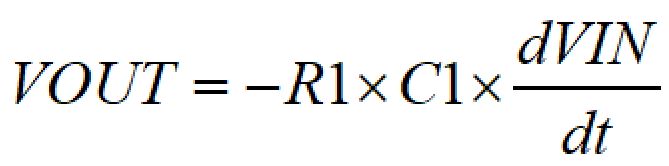
出力電圧が入力電圧の時間微分で表されることが分かりました。
微分回路の計算と波形
前述の計算結果と実際の動作波形が一致することを確認してみます。
下記条件でシミュレーションを行います。
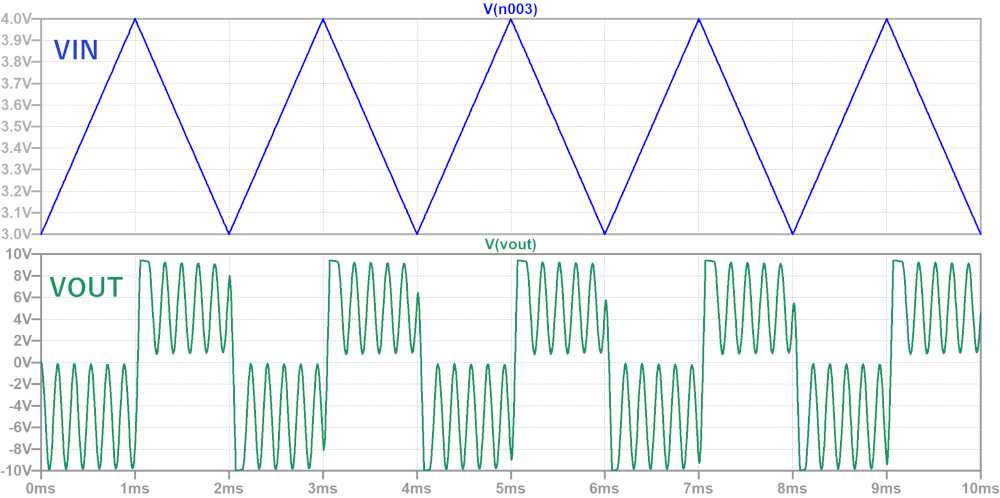
VIN = 3.5V ± 0.5V、500Hzの三角波、C1 = 0.1uF、R1 = 50kΩ
三角波を方形波に変換する回路です。
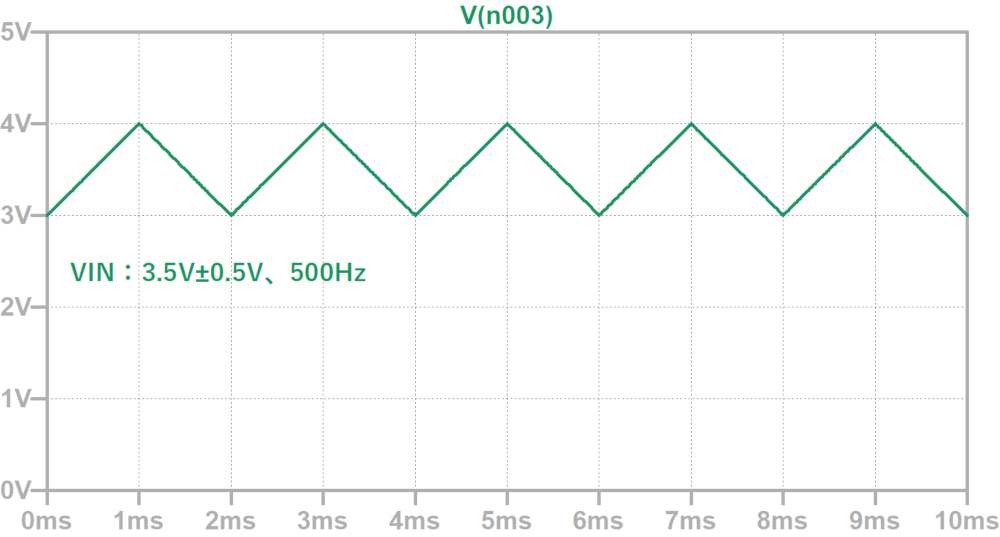
はじめに、上記条件での出力電圧を計算してみましょう。
電圧上昇時の入力電圧を時間:tの関数で表すと、
VIN = t + 3V (tの単位はms)
これをtで微分すると、
dVIN / dt = 1000V/s
となります。
したがって、出力電圧:VOUTは、
VOUT = -RC × dVIN / dt = -50kΩ × 0.1uF × 1000V/s = -5V
となります。
同様に下降時の出力電圧を計算すると、
VOUT = 5V
となります。
シミュレーション波形は下図のようになります。
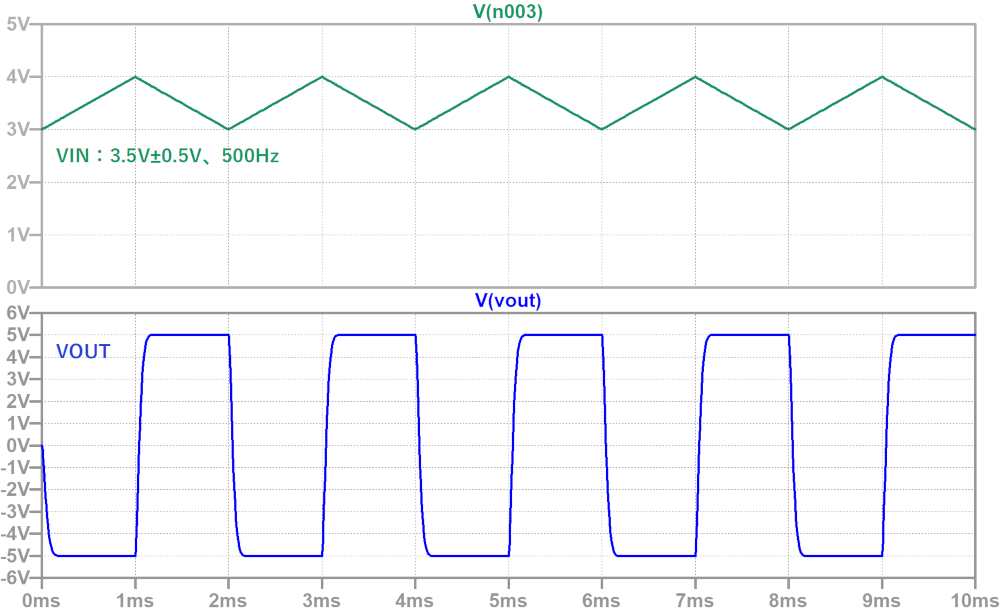
VINが上昇時は-5V、下降時は+5Vの方形波が出力されており、計算結果と一致します。
LTspiceのシミュレーション回路は下記よりダウンロードして頂けます。
微分回路の動作を解説
これまでは数式での計算結果を示してきましたが、ここでは回路の各点の動作波形を見ていきましょう。
各点の電圧、電流グラフを下記に示します。
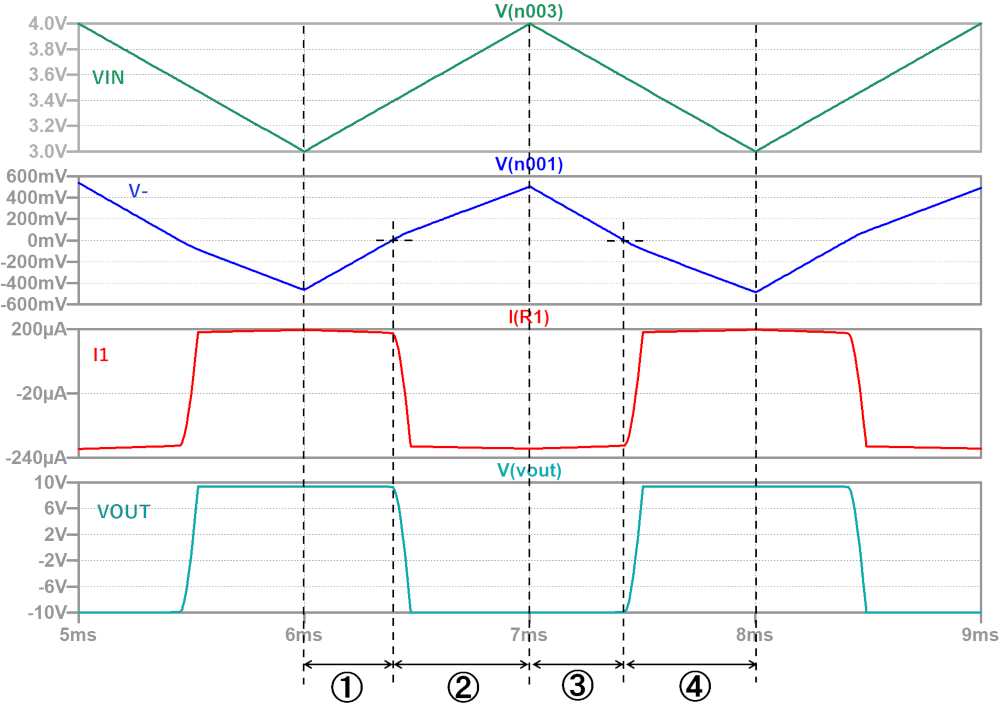
①の領域
V-の電圧はV+より低い状態ですので、出力はHiになります。
VINは上昇し、電流は出力側から入力側に流れ、コンデンサが充電されるため、V-が上昇していきます。
②の領域
V-の電圧がV+(0V)を超えると、出力が反転しLoになります。
VOUTは電流を吸い込むため、V-の電圧上昇の傾きが小さくなります。
③の領域
VINが下降に転じるため、V-の電圧が下降し始めます。
④の領域
V-の電圧がV+より低くなると、出力が再び反転してHiになります。
VOUTは電流を流し出すため、V-の電圧下降の傾きが小さくなります。
微分回路の発振
これまでは基本的な動作原理を説明するための回路で説明してきましたが、実際に動作させると発振してしまうことが多いでしょう。
反転増幅器と同様の考え方で、微分回路の増幅率:GはコンデンサのインピーダンスZcと抵抗R1で決まり、
G = R1 / Zc
となります。
コンデンサのインピーダンスは高周波でゼロに近づくため、増幅率(利得)が大きくなってしまいます。
そのため、実際にはコンデンサC1と直列にRsを挿入し、増幅率の最大値を決めます。
Rsがあることで、コンデンサのインピーダンスがゼロになったとしても、増幅率は、R1 / Rs 以上にはなりません。
周波数特性を確認
Rsの有無で周波数特性がどう変わるか確認しましょう。
まずはRsが無い状態での波形です。
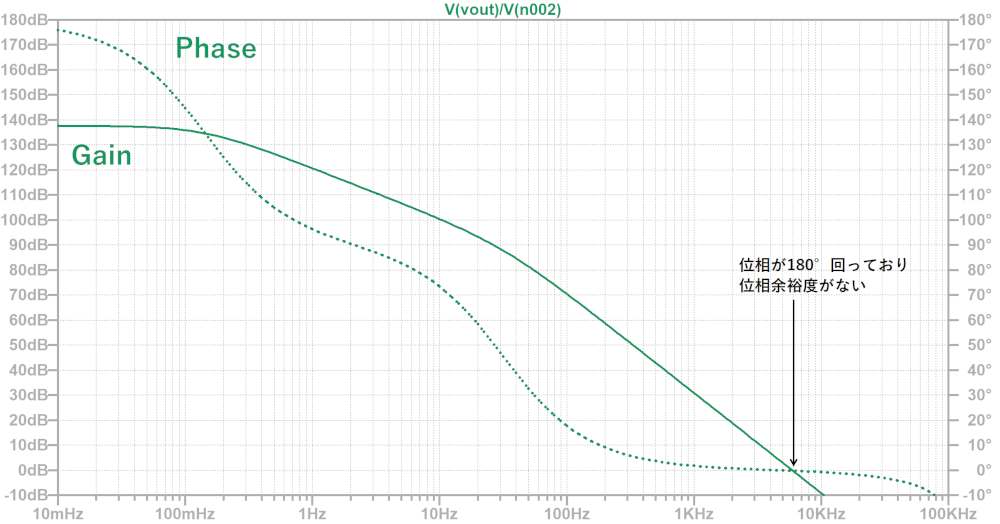
ゲインがある状態で位相が180°回っており、位相余裕度が無いことが分かります。
次に、Rs=1kΩを挿入した状態でAC解析を行いました。
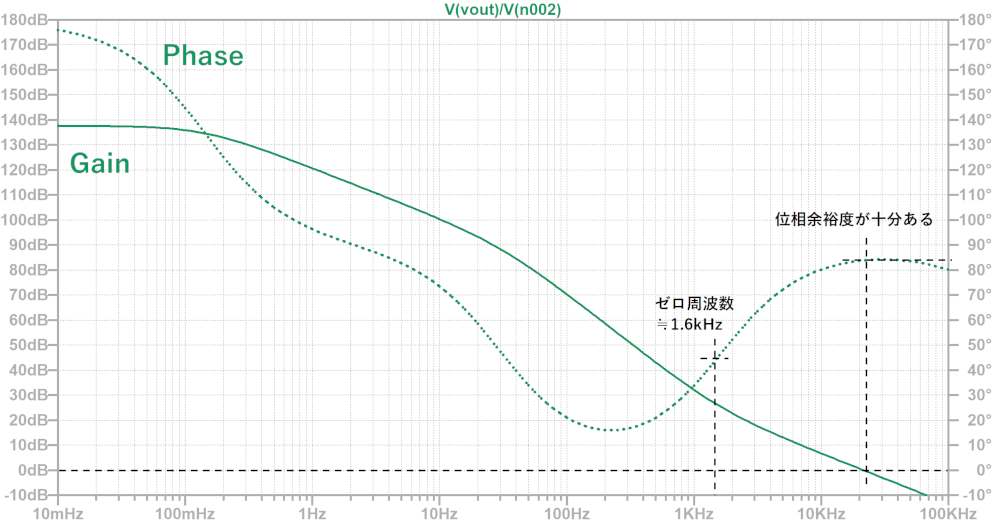
RsとC1でゼロが形成されるため、位相が戻り、位相余裕が十分稼げています。
微分回路と積分回路の違い
微分回路と積分回路の違いをまとめると、以下のようになります。
| 項目 | 微分回路 | 積分回路 |
|---|---|---|
| 回路図 |  |
 |
| 動作 | 入力波形を時間微分した波形を出力 | 入力波形を時間積分した波形を出力 |
| 用途 | ハイパスフィルタ、DC成分除去 | ローパスフィルタ、ノイズ除去 |
微分回路は入力にコンデンサがあるため、高周波成分だけを通すことができます。
逆に積分回路は出力側にコンデンサがあるため、ローパスフィルタとして働き、高周波成分を除去することができます。
本稿では微分回路で三角波を方形波に変換する回路について解説しましたが、積分回路では逆に、方形波を三角波に変換することができます。
